En esta página está contenido un programa (applet) de Java que obtiene la
proyección estereográfica de la tierra a partir de Pe y la distancia entre
Pv y el centro de la tierra, esta distancia está medida en unidades
iguales al radio de la tierra, es decir una distancia igual a 1 significa
que Pv es, de hecho Pe, si la distancia es 2 significa que Pv está alejado
de Pe en un radio terrestre y así sucesivamente.
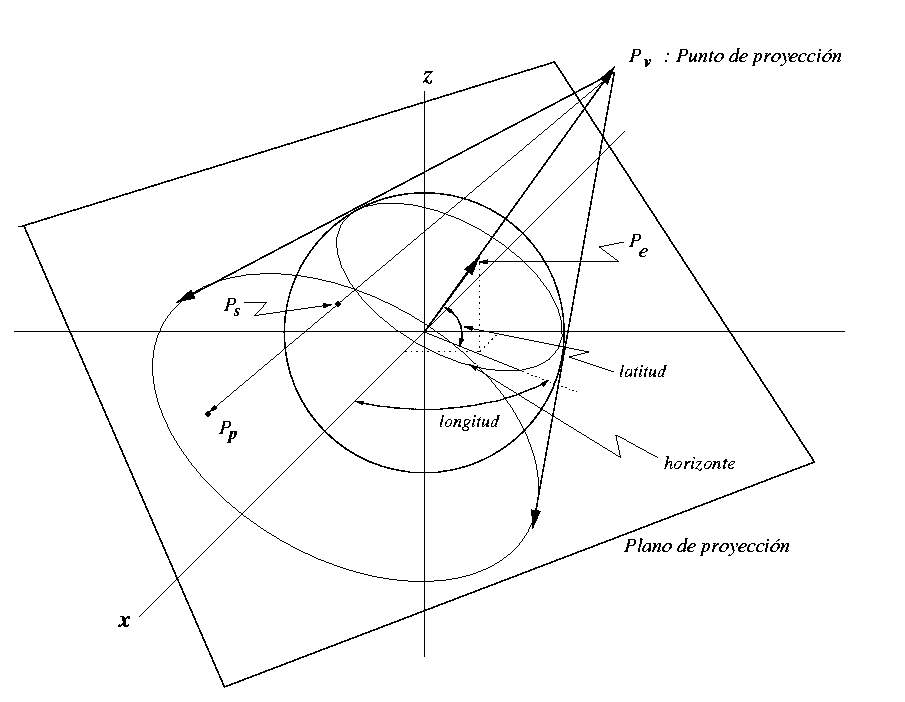
Figura 1: Proyección estereográfica.
El punto Pp sobre el plano, es obtenido proyectando el punto Ps sobre la superficie
de la tierra. Pp está determinado por la intersección del plano con la recta
que pasa por Pv (el punto de proyección) y Ps.
Los rayos que tienen a Pe como centro son tangentes a la tierra en un círculo
al que llamaremos el horizonte. Los puntos que aparecen en el mapa son aquellos
que están más allá del horizonte visible desde Pv.
El punto de proyección queda determinado por:
- Las coordenadas terrestres de un punto sobre la superficie de la tierra
Pe=(longitud, latitud). Como es usual la longitud es un ángulo en grados entre
-180 y 180 y la latitud uno entre -90 y 90. En el punto de proyección está
el zenith de Pe.
- La distancia en radios terrestres entre el centro de la tierra y el punto
de proyección. Se requiere que esta distancia sea mayor que 1.
Cuando el punto de proyección está muy alejado de la tierra (digamos unos
10 radios terrestres) entonces el mapa resultante nos es más o menos
familiar. Pero cuando el punto de proyección está muy cerca de la
superficie terrestre (digamos 1.1 radios terrestres) entonces el conjunto
de puntos que se presentan en el mapa es mucho mayor y podemos ver el
hemisferio norte y sur al mismo tiempo, por ejemplo; algo a lo que no
estamos muy acostumbrados. El aspecto del mapa resultante con el punto de
proyección muy cercano a la tierra es apenas reconocible.
Algunos puntos que pueden servir como ejemplo se muestran a continuación.
Hay que enfatizar que si se quiere que alguno de estos puntos aparezca en el
centro de la proyección, los datos que se deben ingresar en el programa son
los que corresponden a la antípoda del punto deseado; esto hace que el punto
de proyección esté en el zenith de la antípoda.
| Cuidad |
Longitud |
Latitud |
Longitud (antípoda) |
Latitud (antípoda) |
| Beijing |
116 |
39 |
-64 |
-39 |
| Buenos Aires |
-58 |
-35 |
122 |
35 |
| Calcuta |
88.4 |
22.5 |
-91.6 |
-22.5 |
| Johanesburg |
28 |
-26.25 |
-152 |
26.25 |
| México |
-99 |
19 |
81 |
-19 |
| Montreal |
-73.5 |
45.2 |
106.5 |
-45.2 |
| Moscú |
37.6 |
55 |
-142.4 |
-55 |
| Nairobi |
38 |
1 |
-142 |
-1 |
| París |
2.4 |
49 |
-177.6 |
-49 |
| Sydney |
151 |
-34 |
-29 |
34 |
Información técnica
José Galaviz
Gildardo Bautista
