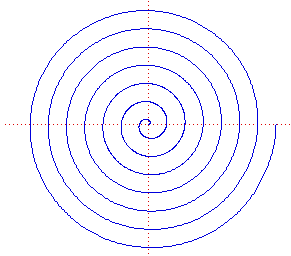
La Espiral de Arquímedes
Otra curva que encontramos en la galería de Curvas Maravillosas es la Espiral de Arquímedes. Esta curva es generada por la combinación de dos movimientos uniformes: uno rectilíneo y otro rotacional, simultáneamente. Es la curva que describiría un escarabajo que camina sobre una regla que rota al mismo tiempo.
La curva que resulta es

La espiral fue estudiada por Arquímedes en su trabajo "Sobre Espirales"
y había sido ya considerada por su amigo Conon que era el astrónomo
de la corte de Tolomeo III, en Alejandría. Arquímedes define la
espiral diciendo:
Si una línea
recta dibujada en un plano gira uniformemente cualquier número de veces
alrededor de un extremo fijo
hasta que regresa a su posición original y si, al mismo tiempo que la
línea gira, un punto se mueve uniformemente a lo largo de la línea
recta comenzando en el extremo fijo, el punto describirá una espiral
en el plano.
Entre la espiral de Arquímedes y la parábola de Apolonio existe una relación notable descubierta por Bonaventura Francesco Cavalieri (1598 -1647), contemporáneo de Galileo, que equivale a trabajo en geometría analítica y cálculo, en tiempos en que ninguno de estos temas había sido formalmente inventado.
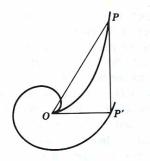
En la figura, el arco OP es un segmento de parábola y la distancia OP', definida por la primera vuelta de la espiral, es el radio de un círculo con centro en O. Si la distancia PP' se toma como la circunferencia del círculo de radio OP', el área dentro de la primera vuelta de la espiral es exactamente igual al área entre el arco parabólico OP y el radio vector OP'. Contrástese este resultado con la primera proposición de Arquímedes de su libro "Mediciones del Círculo", que dice:
El área de un círculo es igual al triángulo rectángulo
que tiene los lados más cortos iguales al radio del círculo y
a la circunferencia del círculo. De manera que el área del círculo
con radio OP es igual al área del triángulo OPT.
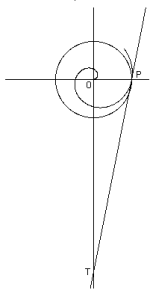
El punto T queda fijo al intersecarse la tangente a la espiral en el punto P con la prolongación del eje vertical. La distancia PP' de la figura de Cavalieri equivale a la distancia OT del dibujo de Arquímedes, ambas son la circunferencia del círculo de radio OP.
Arquímedes fue capaz
de calcular la longitud de varias tangentes a la espiral y mostró que
puede ser usada para trisecar un ángulo y cuadrar
el círculo, dos de los tres problemas clásicos de la antigüedad.
Nota: En esta dirección hay un java que te permite jugar con la espiral y sus curvas asociadas: http://www-history.mcs.st-and.ac.uk/history/Java/Spiral.html
Hablando de equivalencias a trabajo en cálculo, ¿sabías que la primera integración la hizo Arquímedes al calcular el área bajo un segmento de parábola? Los métodos que utilizaba mezclaban conceptos geométricos y mecánicos estrechamente. En su obra "La Cuadratura de la Parábola" demuestra que el área de un segmento de parábola es igual a 4/3 del área del triángulo inscrito. Para una parábola (cuya ecuación cartesiana general es: y = ax2 + bx + c),
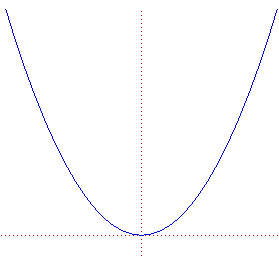
calcularemos la 'cuadratura' de acuerdo al método de Arquímedes.
En la imagen, el segmento de parábola mostrado tiene inscrito un triángulo t0. En los dos segmentos restantes se inscriben dos triángulos de igual base y altura, t01 y t02. Sea su suma t1. En los cuatro segmentos de parábola que se forman, se inscriben los triángulos t11,t12, t13, t14.
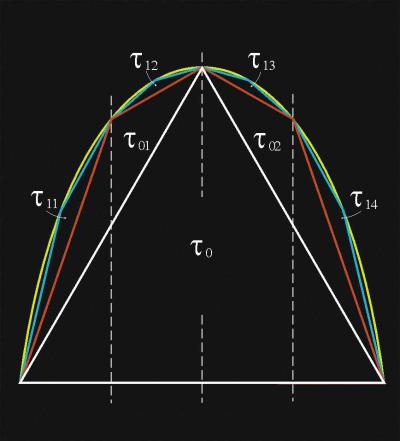
Sea su suma t2. Se demuestra fácilmente
que, t0 = 4t1, t1
= 4t2, y así, sucesivamente.
Los espacios que restan de los triángulos se hacen cada vez más
pequeños pero siempre se mantiene que cada uno es igual a ¼ del
precedente. Basta notar que, el polígono que se construye de esta forma,
se aproxima efectivamente al segmento de parábola y que t1
= 1/4t0 ; t2 = 1/42t0
; t3 = 1/43t0 ...
Por tanto, t0 + t1 + t2
+ t3 + ... = 4/3t0. La demostración 'mecánica',
controlaba por peso la proporción entre los triángulos. La 'geométrica'
se redujo a la suma de una serie, la que ahora conocemos como la serie geométrica:
1 + x + x2 +....+ xn.
Para el caso x<1 esta serie se escribe como: 1+ x + x2
+ ..... = 1/(1-x). En el caso x = 1/4, se tiene: 1/(1-1/4) = 1/(3/4)
= 4/3. Esto es, el segmento de parábola = 4/3t0.
En el contexto de la matemática griega, la suma no se podía obtener de una demostración directa ya que, en este caso, se trataba de una suma infinita y esto no era aceptable. Se recurría entonces a métodos de 'reducción al absurdo'. Arquímedes postuló: "Dadas dos superficies desiguales, el exceso por el cual la mayor supera a la menor, puede ser sumado consigo mismo resultando más grande que cualquier superficie asignada". Este postulado se conoce como de Eudoxo - Arquímedes. En su cuadratura fue necesario un doble absurdo: notar que el segmento parabólico no puede ser ni mayor ni menor que 4/3t0; demostró que tenía que ser precisamente 4/3t0. Las áreas del segmento de parábola y la del triángulo t0 son entonces conmensurables entre sí y es una cuestión sencilla de geometría elemental construir un cuadrado igual a 4/3t0 con regla y compás. De aquí que el segmento de parábola se haya "cuadrado".
En el prefacio a su tratado sobre la cuadratura de la parábola Arquímedes escribe: "Muchos matemáticos han intentado cuadrar el círculo, la elipse, o el segmento de una elipse o de una hipérbola, y el edificio de lemas que construyeron para este propósito, ha estado abierto a objeciones en general. Ninguno, sin embargo, parece haber pensado en intentar la cuadratura de un segmento delimitado por una recta y una sección de cono rectángulo (una parábola) la cual es, precisamente, la que sí se puede calcular y que yo sí he encontrado".
Arquímedes de Siracusa (ca. 287-212 a. C.) fue, quizás, el matemático más grande de la antigüedad y es, sin duda, uno de los grandes de todos los tiempos. Su creatividad se manifestó en la producción de numerosas invenciones, todas maravillas de su época; el esclarecimiento de principios científicos y las aplicaciones de las matemáticas. Arquímedes estaba especialmente orgulloso de haber descubierto que si un cono se contenía en una esfera que, a su vez, estaba contenida en un cilindro, los volúmenes de los tres sólidos estaban en la relación 1:2:3. La relación fue grabada en su tumba. Por desgracia, la localización y autenticidad de dicha tumba, es incierta.