
Unidades 4.4 y 5.4
Probabilidad: Eventos independientes y eventos mutuamente excluyentes
RES
Propósito
Que el alumno conozca los conceptos básicos de la Teoría de Probabilidades, que pueda distinguir en diversas situaciones de azar eventos que son independientes o mutuamente excluyentes y que reflexione sobre la Ley Débil de los grandes números.
Instrucciones generales
La unidad se divide en cinco apartados:
- Conjuntos
- Azar
- Probabilidad
- Eventos
- Ley Débil
Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.

Los tres botones que se encuentran en la parte derecha tienen la función siguiente:
 |
Brinda acceso a la ayuda de las escenas interactivas |
 |
Herramientas de Enciclomedia |
 |
Cerrar la ventana |
En principio se accede al experimento con una urna y bolas de billar, pero en la escena Azar 1 se puede cambiar a otros dos ejemplos, uno con dados y otro con una ruleta. El funcionamiento de los tres experimentos es análogo, por lo cual sólo se incluye la explicación del primero.
1. Conjuntos
Este apartado tiene cuatro escenas.
Notación y representación
El objeto de la primera escena es que el alumno conozca la representación gráfica y la notación de conjuntos. En una mesa de billar aparecen seis bolas y unos círculos marcados asemejando un diagrama de Venn. Hay que arrastrar las bolas hacia los círculos para representar dos conjuntos, A y B. Del lado izquierdo se puede observar la notación correspondiente al diagrama incluyendo la unión y la intersección de los conjuntos. Con los botones Ver/Ocultar se puede ocultar o volver a mostrar cada uno de los círculos. Oprímase el botón Otra vez para reiniciar la aplicación.
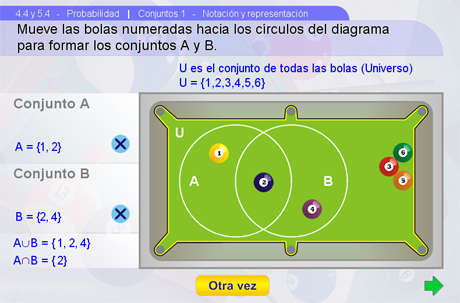
Sugerencias didácticas
Es importante hacer notar el significado de que una bola esté en cada región delimitada por los círculos incluyendo el exterior de ambos. Se puede trabajar al principio con sólo una bola, posteriormente con dos, e ir incrementando el número de bolas en juego para una asimilación gradual de los conceptos de conjuntos.
Descripción de conjuntos 1
En la segunda escena el alumno observará que los conjuntos se pueden describir por medio de las propiedades de sus elementos. Con los respectivos pulsadores se puede navegar entre algunos posibles conjuntos formados con las bolas de billar, descritos mediante las propiedades de sus elementos. Con los botones Ver/Ocultar se muestra la notación correspondiente a los conjuntos elegidos, así como su representación gráfica en la mesa de billar.
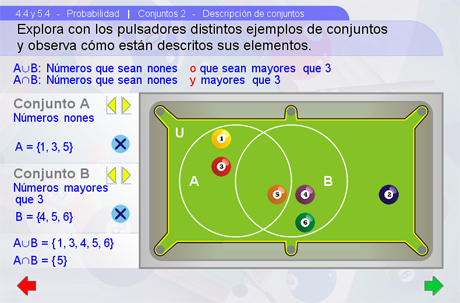
Sugerencias didácticas
Hay que recalcar el hecho de que un conjunto puede definirse de dos formas equivalentes: enumerando sus elementos o describiéndolos mediante una condición. Luego, hay que hacer énfasis en el hecho de que los elementos en la unión deben cumplir al menos una de las condiciones, y los elementos en la intersección deben cumplir ambas condiciones.
Descripción de conjuntos 2
Mediante la siguiente escena, se tiene la libertad de construir una pareja de conjuntos para después describirla con palabras. Hay que arrastrar las bolas de billar hacia los círculos para formar los conjuntos A y B, automáticamente se muestra su notación en la parte izquierda. Luego hay que escribir mediante el plumón electrónico una descripción con palabras de cada conjunto, de la unión y de la intersección.
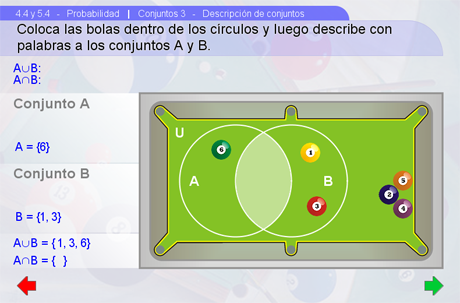
Sugerencias didácticas
En esta escena es conveniente motivar a los alumnos a encontrar patrones entre las diferentes bolas de un conjunto que permitan describirlo sin necesidad de enumerar a todos sus elementos. También es importante hacer notar la conveniencia de usar la conjunción "y" o la disyunción "o" para expresar la intersección o la unión, respectivamente.
Ejercicio
En la siguiente escena, el alumno practicará los temas expuestos mediante un ejercicio en el que deberá representar adecuadamente una pareja de conjuntos. Del lado izquierdo aparece la descripción de dos conjuntos. Hay que arrastrar las bolas hacia los círculos de tal manera que representen adecuadamente los conjuntos A y B indicados. Mediante los botones Ver/Ocultar se muestra la notación de cada conjunto. Para comprobar que el ejercicio se resolvió correctamente se debe presionar el botón Verificar, el ejercicio se repite las veces necesarias para que la Barra Jinich se complete.
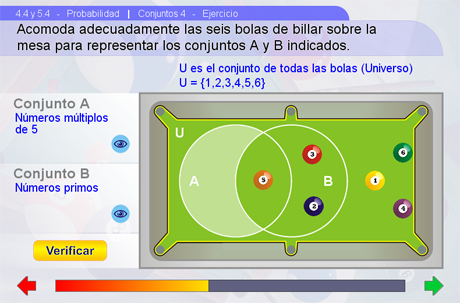
Sugerencias didácticas
Aquí se pueden practicar distintas técnicas para construir los conjuntos indicados. Una puede ser construir el conjunto A y despues el B, moviendo los elementos repetidos hacia la intersección. Otra puede ser construir primero la intersección observando cuáles elementos cumplen ambas condiciones, y después completar ambos conjuntos con los elementos que cumplan alguna de las dos condiciones.
2. Azar
Este apartado tiene cuatro escenas.
Experimento aleatorio
En esta escena el alumno se familiarizará con el experimento aleatorio que consiste en extraer al azar una de las seis bolas de billar colocadas en una urna. Mediante el botón Extraer se simula una realización del experimento. Para volver a las condiciones iniciales oprímase el botón Nuevo.
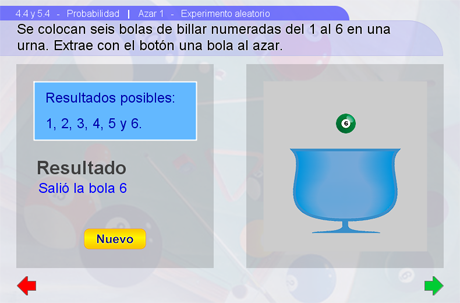
Sugerencias didácticas
En esta escena el alumno debe familiarizarse por completo con las características del experimento aleatorio. Deberá ser consciente de que en la urna hay seis bolas de billar numeradas, que se debe extraer una al azar y no es posible saber, de antemano, cual saldrá. También debe convencerse de que hay exactamente seis resultados posibles y saber cuáles son.
Eventos del experimento 1
En esta escena se exploran los diferentes eventos posibles para el experimento aleatorio. Mediante el menú de la parte izquierda se puede navegar por los eventos y elegir uno de ellos (colocándolo en el rectángulo azul). En la parte derecha aparece el espacio de resultados en donde se resaltarán aquellos que pertenezcan al evento elegido.
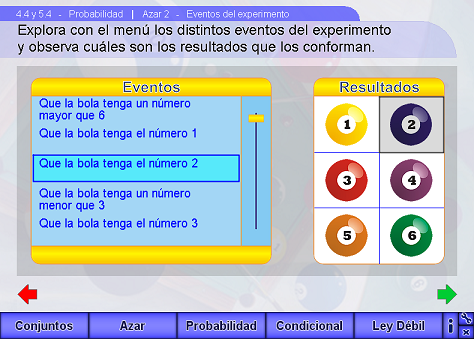
Sugerencias didácticas
Aquí el alumno deberá comprender que un evento puede englobar a varios resultados posibles. Es importante hacer notar que un resultado es diferente al evento que puede contener sólo a ese resultado o a varios. Por ejemplo, el evento "que la bola tenga el número 2" contiene sólo al resultado consistente en que la bola sacada tiene el 2. El evento, en cambio, "que la bola tenga un número par menor que el 5" incluye los resultados: "salió la bola con el 4" y "salió la bola con el 2".
Eventos del experimento 2
En esta escena hay que relacionar la descripción de un evento con su notación como conjunto. Del lado izquierdo aparecen las descripciones y del lado derecho las respectivas notaciones pero en desorden. Hay que arrastrar las notaciones hacia la tabla de la izquierda a la altura del evento correspondiente. Una vez que se ha llenado la tabla se activa el botón Verificar, hay que presionarlo para saber si la asociación se hizo correctamente, del lado derecho aparece una paloma para cada asociación correcta y un tache para las incorrectas. Si hay errores se deben corregir hasta que la tabla quede adecuadamente llena. Una vez que no se tienen errores se activa el botón Otra vez, presiónese para trabajar con otra tabla similar.

Sugerencias didácticas
Es importante que los alumnos identifiquen las palabras clave "y" y "o" para conocer los resultados que pertenecen al evento descrito. También se pueden practicar estrategias de deducción como la eliminación de los conjuntos que no cumplan una propiedad, para llegar al único que sí la cumple.
Ejercicio
En la siguiente escena, el alumno practicará los temas expuestos mediante un ejercicio en el que deberá indicar cuáles de los eventos indicados se han cumplido al realizar el experimento. En una primera instancia, mediante el botón Realizar se simula la realización del experimento aleatorio; luego, se deben selecciónar en la tabla de la izquierda cuáles de los eventos se cumplieron. Para comprobar que el ejercicio se resolvió correctamente se debe presionar el botón Verificar, el ejercicio se repite las veces necesarias para que la Barra Jinich se complete.
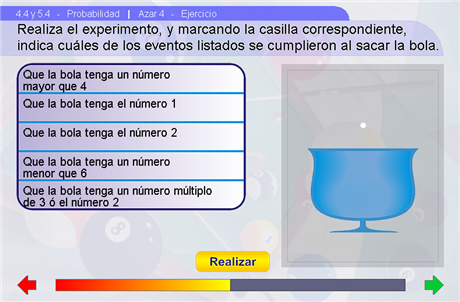
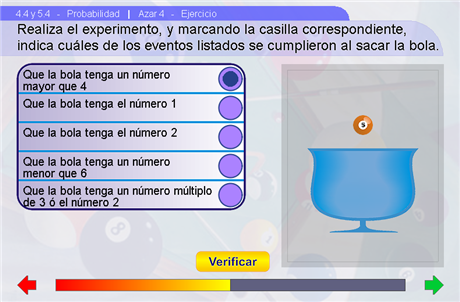
Sugerencias didácticas
Aquí es muy importante que el alumno comprenda que para que un evento se cumpla debe suceder alguno de los resultados que contiene. También se debe hacer notar que al realizar el experimento el resultado puede pertenecer a más de un evento a la vez.
3. Probabilidad
Este apartado tiene tres escenas.
Eventos del experimento
En esta escena el alumno debe identificar cuáles de los resultados están contenidos en un evento elegido y notar cuántos son los casos favorables de tal evento. Con el menú del lado izquierdo se elige un evento (colocándolo en el rectángulo azul) y en el espacio de resultados del lado derecho se deben resaltar, haciendo clic sobre ellos, los resultados contenidos en el evento. Para verificar que la actividad se realizó correctamente hay que presionar el botón Verificar. Si no hay errores aparecerá un mensaje indicando cuántos son los casos favorables, en caso contrario se indica el error y habrá de hacer las correcciones necesarias. Para repetir la actividad hay que presionar el botón Nuevo.

Sugerencias didácticas
Se debe familiarizar al alumno con la noción de caso favorable, indicando que una vez elegido un evento, será un éxito obtener en el experimento alguno de los resultados que contiene, y un fracaso obtener algún otro resultado no contenido en el evento.
Probabilidad de eventos
En esta escena se aborda el cálculo de la probabilidad de un evento. En primera instancia hay que elegir uno de los eventos con el menú de la izquierda (colocándolo en el rectángulo azul y presionando Elegir). Una vez elegido un evento, aparecerá una pantalla con el enunciado del evento y su probabilidad, además del espacio de resultados con los resultados contenidos en el evento resaltados. Mediante el botón Ver/Ocultar se muestran los elementos mediante los cuales se puede calcular la probabilidad del evento, así como la notación de este último. Para repetir la escena y elegir otro evento hay que presionar el botón Nuevo.

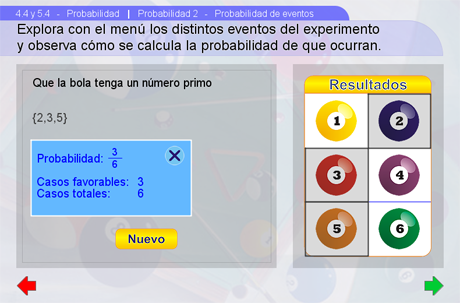
Sugerencias didácticas
Aquí es importante hacer notar que la probabilidad de determinado evento se calcula como un cociente: el número de casos favorables entre el número total de casos posibles. Por ejemplo, si el evento se define como "sacar una bola con el 1 ó un número igual o mayor que 5", la probabilidad de que ocurra se calcula como el número de casos favorables que es 3 (sacar el 1, el 5 ó el 6) dividido por el número total que es 6. Es decir, 3/6=1/2.
También es conveniente hacer hincapié en que la probabilidad sólo está definida para los eventos y no para los resultados individuales.
Ejercicio
En la siguiente escena, el alumno practicará los temas expuestos mediante un ejercicio en el que deberá indicar cuál es la probabilidad del evento E indicado. Por medio de los pulsadores deberá expresar la probabilidad de E como un cociente. Con el botón Ver/Ocultar se puede observar la notación del evento; además, las bolas de billar en la urna se pueden manipular para aclarar cuáles y cuántos son los casos favorables. Para comprobar que el ejercicio se resolvió correctamente se debe presionar el botón Verificar, el ejercicio se repite las veces necesarias para que la Barra Jinich se complete.
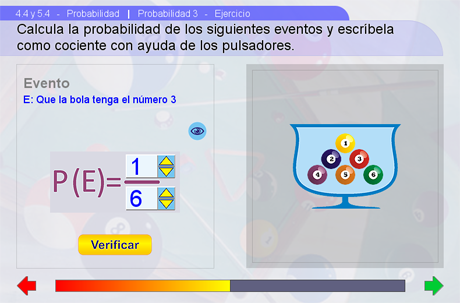
Sugerencias didácticas
En esta escena es conveniente hacer notar que con fracciones equivalentes se puede expresar la misma probabilidad. Además, se puede trabajar la intuición como al observar que si la mitad de los resultados son favorables, entonces la probabilidad es un medio.
4. Eventos
Este apartado tiene tres escenas.
Eventos mutuamente excluyentes
En esta escena se le muestra al alumno la condición para que dos eventos sean mutuamente excluyentes. En una primera instancia, por medio del menú de la izquierda se deben elegir dos de los eventos del experimento. Con el botón Evento A se elige un primer evento el cuál quedará resaltado en el espacio de resultados de la derecha, luego, con el botón Evento B se elige un segundo evento el cuál también quedará resaltado en el espacio de resultados. Cada evento es resaltado con el color del botón correspondiente. Para corregir el evento elegido hay que presionar el botón Limpiar. Una vez elegidos ambos eventos aparece una pantalla con la descripción de los eventos y la intersección. En la parte inferior se indica si la intersección es o no vacía y la implicación de ello. Con los botones Ver/Ocultar se puede ocultar uno de los eventos para poder analizar el otro individualmente. Con el botón Nuevo se regresa al menú para elegir otro par de eventos.
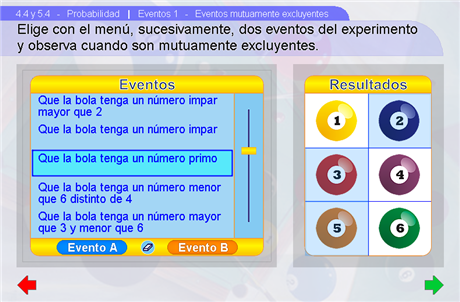

Sugerencias didácticas
Aquí se puede hacer notar que para identificar eventos excluyentes no es necesario calcular sus probabilidades. También se puede mencionar el hecho de que en los mismos enunciados que describen los eventos se puede notar cuándo éstos son excluyentes.
Eventos independientes
En esta escena se le muestra al alumno la condición para que dos eventos sean independientes. En una primera instancia, por medio del menú de la izquierda se deben elegir dos de los eventos del experimento. Con el botón Evento A se elige un primer evento el cuál quedará resaltado en el espacio de resultados de la derecha, luego, con el botón Evento B se elige un segundo evento el cuál también quedará resaltado en el espacio de resultados. Cada evento es resaltado con el color del botón correspondiente. Para corregir el evento elegido hay que presionar el botón Limpiar. Una vez elegidos ambos eventos aparece una pantalla con la descripción de los eventos y la intersección, así como sus respectivas probabilidades. En la parte inferior se indica el producto de las probabilidades de A y B, si este producto es o no igual a la probabilidad de la intersección y la implicación de ello. Con los botones Ver/Ocultar se puede ocultar uno de los eventos para poder analizar el otro individualmente. Con el botón Nuevo se regresa al menú para elegir otro par de eventos.
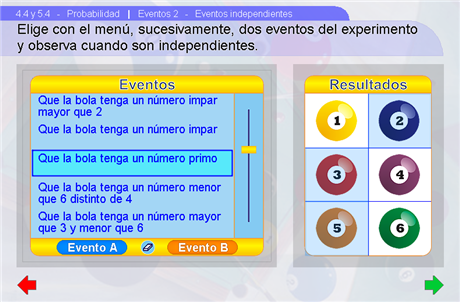

Sugerencias didácticas
Es importante aclarar a los alumnos el significado de la independencia de eventos. Dos eventos son independientes cuando la ocurrencia de uno no afecta la probabilidad de ocurrencia del otro. Esto se puede ilustrar con ejemplos concretos como los siguientes:
Supongamos que un experimento consiste en extraer una bola de una urna que contiene seis bolas, numeradas del 1 al 6.
Consideremos dos eventos. A: "La bola extraída tiene un número par" y B: "La bola extraída tiene un número menor que 4". Antes de sacar la bola, la probabilidad de A es 3/6 pues hay tres bolas pares en la urna y la probabilidad de B es 3/6 pues hay 3 bolas con números menores que 4.
Imaginemos ahora la siguiente situación. Juan saca una bola, ve el número y le informa a Claudia que se trata de un número par. Le pregunta entonces ¿cuál es la probabilidad de que el número sea menor que 4?
Claudia sabe que la bola extraída sólo puede tener el 2, el 4 ó el 6, y de estos números, sólo el 2 es menor que 4. Por lo tanto, la probabilidad de B resulta ser ahora 1/3. Note que, sin la información parcial dada por Juan, Claudia hubiera dicho que la probabilidad de B era 3/6=1/2, sin embargo, ahora contesta que esta probabilidad es 1/3. Por este motivo, A y B no son independientes, la ocurrencia de uno afecta la probabilidad de ocurrencia del otro.
Los eventos C: "La bola tiene un número del 1 al 6" y D: "La bola tiene un número impar" son independientes, pues el hecho de saber que ocurrió C no afecta la probabilidad de ocurrencia de D y viceversa.
Los eventos E: "La bola tiene un número impar distinto de 3" y F: "La bola tiene un número par mayor que 3 ó el número 1" son también independientes, nuevamente, el hecho de saber que ocurrió E no afecta la probabilidad de ocurrencia de F y viceversa.
Es importante hacer notar que para identificar eventos independientes es necesario calcular las probabilidades de los eventos y también la de su intersección.
Por ejemplo, en el caso de los eventos E y F, tenemos que E={1,5}, F={4,6,1} y la intersección de los dos eventos es EF={1}, de donde:
P{E}=2/6=1/3
P{F}=3/6=1/2
P{EF}=1/6
P{E}P{F}=(1/3)(1/2)=1/6=P{EF}
Así, los eventos E y F son independientes ya que el producto de sus probabilidades es igual a la probabilidad de su intersección. Resumiendo, ésta es precisamente la definición de eventos independientes.
Definición: dos eventos E y F son independientes cuando P{E}P{F}=P{EF}.
Ejercicio
En la siguiente escena, el alumno practicará los temas expuestos mediante un ejercicio en el que deberá indicar si dos eventos propuestos son o no independientes. Si los eventos son independientes debe presionar el botón Sí, y en caso contrario debe presionar el botón No. Con el botón Ver/Ocultar se puede observar la notación de cada evento y su probabilidad, además de su representación en el espacio de resultados. El ejercicio se repite las veces necesarias para que la Barra Jinich se complete.
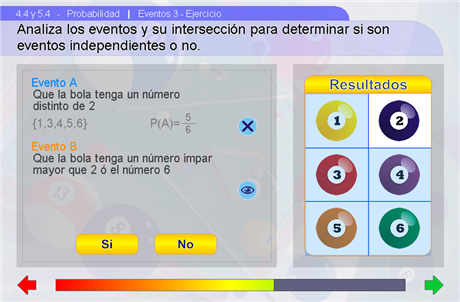
Sugerencias didácticas
Es preferible no mostrar la ayuda a menos que haya demasiados problemas para calcular las probabilidades o para encontrar la intersección de los eventos. Es recomendable ayudarse del espacio de resultados para motivar una idea gráfica de los eventos.
5. Ley Débil
Este apartado tiene dos escenas.
Frecuencia relativa
En esta escena el alumno reflexionará sobre lo que ocurre con la frecuencia relativa de los eventos al repetir varias veces un experimento aleatorio. Mediante los pulsadores podrá elegir cuántas repeticiones del experimento se realizarán al presionar el botón Ejecutar Experimento. Del lado derecho se irá graficando la frecuencia relativa de los eventos consistentes en cada uno de los seis resultados individuales del experimento, y del lado izquierdo aparecerá una tabla que indica el número de veces que ha ocurrido cada evento y su frecuencia relativa. Con el botón Limpiar la gráfica y la tabla regresan a su estado inicial. Con el botón Ver/Ocultar se muestra una línea que ayuda a medir con mayor precisión los resultados en la gráfica.
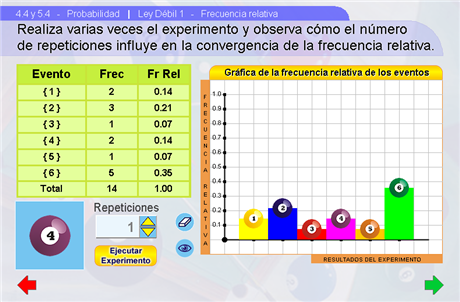
Sugerencias didácticas
Es importante hacer notar cómo la probabilidad expresa una proporción entre el número de veces que se realiza un experimento y el número de veces que se espera obtener cada resultado.
Convergencia
En esta escena el alumno reflexionará sobre la convergencia de la frecuencia relativa de la ocurrencia de un evento hacia la probabilidad del mismo. Mediante los pulsadores podrá elegir cuántas repeticiones del experimento se realizarán al presionar el botón Ejecutar Experimento. Del lado derecho se irá graficando la frecuencia relativa del evento indicado en la parte superior como éxito. Del lado derecho se irá graficando la frecuencia relativa de la ocurrencia del evento y del lado izquierdo aparecerá una tabla indicando el número de veces que ha ocurrido el evento y su frecuencia relativa. Una vez realizada una serie de catorce extracciones, quedará un rastro en la gráfica y se activará el botón Nuevo para comenzar otra serie. Con el botón Limpiar se eliminan los rastros que dejan las diferentes series de repeticiones. Con el botón Ver/Ocultar se pueden dejar de ver momentáneamente estos rastros. Para cambiar el evento indicado como éxito hay que presionar el botón Cambiar.

Sugerencias didácticas
Aquí se puede introducir de manera intuitiva y sin mucha profundidad la noción de límite y reflexionar sobre distintas maneras de aproximar la probabilidad de un evento en el experimento aleatorio con base en sucesivas repeticiones del mismo.
Créditos
AutorCarlos Alberto Serrato Hernández
Reconocimientos
A Ángela Núņez Castaín en cuyo trabajo se inspiró la parte gráfica de la escena Ley Débil 2 - Convergencia http://descartes.cnice.mec.es/materiales_didacticos/monedas/monedas.htm
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes.
Como la unidad utiliza el applet Descartes, propiedad del Ministerio de Educación de España,
sus contenidos se distribuyen bajo una licencia de
