Más abajo, presentamos los pasos para realizar este proceso iterativo, y en el marco de la derecha, dando clic sobre los botones con las etiquetas P1, P2, P3, . . . se van mostrando los trazos correspondientes.

Para interrumpir la animación, da clic en el botón Animar/Parar.

Para construir las curvas que dan lugar a la que se muestra, da clic en el botón Iniciar construcción.

Construcción:

P1. Partimos de un triángulo equilátero.

P2. Dividimos cada lado del triángulo en tres segmentos iguales, y sobre cada segmento central, construimos un triángulo equilátero (hacia afuera).

P3. Ocultamos el segmento central de cada lado. La curva resultante, es un polígono estrellado de 12 lados.

Repetimos el proceso.

P4. Dividimos cada lado del polígono anterior, en tres segmentos iguales, y sobre cada segmento central, construimos un triángulo equilátero (hacia afuera).

P5. Ocultamos el segmento central de cada lado. La curva resultante, es un polígono estrellado de 48 lados.

Repetimos el proceso.

P6. Dividimos cada uno de los lados del polígono anterior, en tres segmentos iguales, y sobre cada segmento central, construimos un triángulo equilátero (hacia afuera).

P7. Ocultamos el segmento central de cada lado. La curva resultante, es un polígono estrellado de 192 lados.

La curva Copo de Nieve, es la curva límite, resultante de este proceso iterativo.

Una característica interesante:

Aunque la Curva de Koch encierra un área finita, su "longitud" es infinita.

Ya que, si dibujamos un círculo circunscrito al triángulo equilátero (da clic en el botón Mostrar circuncírculo), y realizamos el proceso iterativo, el área encerrada por cada figura permanecerá siempre dentro del círculo, y por lo tanto, el área encerrada por el Curva de Koch, también.

Así, el área encerrada por la Curva de Koch es menor que el área del círculo.

Por otro lado, si la longitud de cada uno de los lados del triángulo inicial es L, entonces su perímetro será 3L.

Y en cada iteración, se estarán removiendo los segmentos centrales de cada lado y se estarán agregando dos segmentos de la misma longitud del removido.

Por lo tanto, se estará sustituyendo cada lado, por cuatro lados mas pequeños de longitud total 4/3 de la longitud del lado sustituido.

Así, el nuevo perímetro, será 4/3 del perímetro anterior.

Por lo tanto, los perímetros de los polígonos de cada iteración, serán:

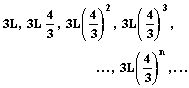
Y la diferencia entre dos de estos perímetros consecutivos, será:

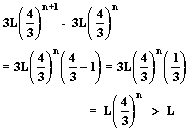
Es decir, los perímetros consecutivos, crecen en más que L, y así "tienden" a infinito.