2  Rotando para simplificar

Igual que la proyección cilíndrica, a la que estamos habituados, la proyección estereográfica permite trazar mapas de la tierra, aunque de aspecto posiblemente muy extraño.

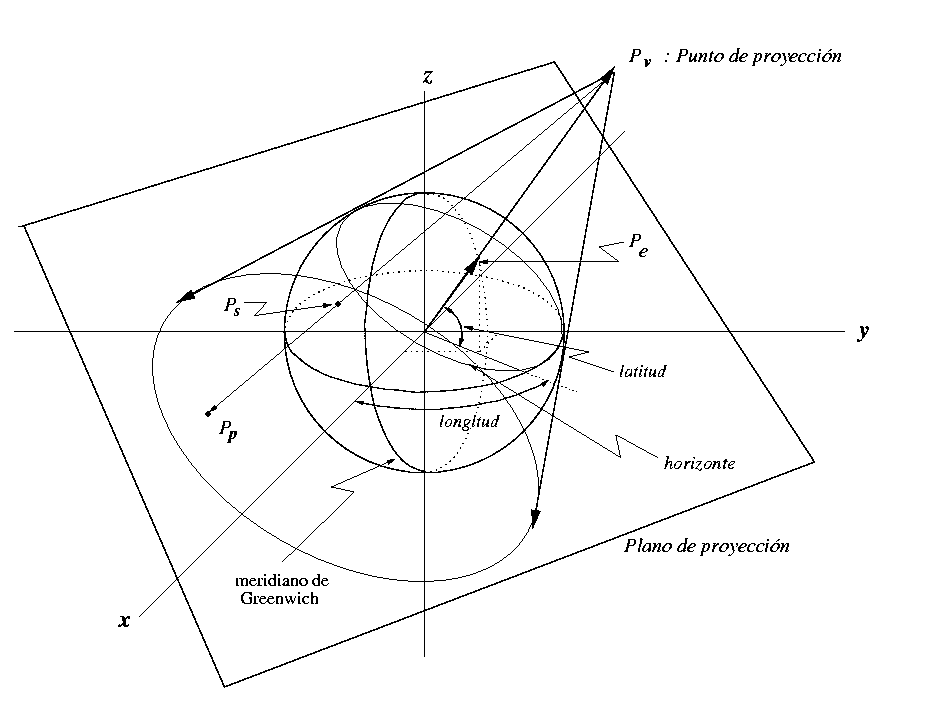
Para efectuar la proyección estereográfica se requiere, además de la tierra (el objeto a proyectar), de los siguientes elementos (ilustrados en la figura 1):

1. Un punto exterior a la tierra, al que llamaremos en lo sucesivo el punto de proyección y denotaremos con P_v. La distancia entre este punto y el centro de la tierra, es decir el origen (0,0,0), la denotaremos con d_p. La recta que pasa por P_v y el origen, atraviesa la tierra, intersecta la superficie de la esfera en dos puntos: con P_e denotaremos el más cercano a P_v y con P¢_e denotaremos el opuesto (el punto antípoda de P_e). El cono con vértice P_v y tangente a S²2, la intersecta en un círculo al que llamaremos el horizonte, todos los puntos sobre este círculo distan d_h de P_v. De hecho los puntos de S²2 cuya distancia a P_v es mayor o igual a d_h no son visibles desde P_v, aquellos que distan menos de d_h sí lo son.

2. Un plano de proyección P sobre el que se proyectan los puntos de S²2 cuya distancia a P_v es mayor que d_h. Este plano contiene a P¢_e y la recta que pasa por P¢_e, el origen, P_e y P_v es normal a él.

Dado un punto arbitrario en S²2 P_s = (x_s,y_s,z_s), tal que d(P_s, P_v) ³ d_h, lo primero que se requiere es encontrar el punto P_p = (x_p, y_p, z_p) en P que resulta de proyectar a P_s. Esto consiste en encontrar las ecuaciones del plano, de la recta que pasa por P_v y P_s y hallar la intersección de ambos. Pero esto tiene el inconveniente de que, en el futuro, cuando queramos calcular al factor de escalamiento necesario para generar un mapa de tamaño arbitrario no sabremos exactamente como enviar P_p al mapa; necesitaríamos definir un orden parcial en el conjunto de puntos proyectados, para lograr esto lo más fácil es enviar P al plano xy para así saber exactamente, para cada punto, que tan "lejos de la orilla del mapa" está. Pero podemos simplificar el problema si de antemano rotamos la esfera completa de tal forma que el punto P_v quede sobre el eje z; así ya sabemos muchas cosas y las ecuaciones de P y las rectas son mucho más sencillas, lo que facilita calcular las intersecciones y evita el problema mencionado a la hora de enviar los puntos proyectados al mapa final.

Ahora bien ¿cuánto hay que rotar la esfera para hacer que P_v quede sobre el eje z? P_v está definido por tres elementos, de hecho la entrada del algoritmo que estamos construyendo, a saber: las coordenadas del punto sobre la tierra que está directamente "abajo" de P_v, es decir las coordenadas terrestres de P_e y la distancia entre P_v y el centro de la tierra, es decir d_p. Las coordenadas terrestres de P_e son una pareja (lon, lat) como las descritas anteriormente, la distancia d_p, por conveniencia, la especificaremos en radios terrestres, es decir d_p=1 significa que P_v=P_e, d_p=2 significa que P_e dista lo mismo del centro de la tierra que de P_v (P_v está a dos radios terrestres del centro de la tierra).

Si lo que deseamos es llevar el punto P_v al eje z entonces también P_e = (lon, lat) quedará sobre el eje z y de hecho sus coordenadas rectangulares serán (0,0,1). Esto significa rotar la tierra hasta que P_e quede donde antes estaba el polo norte. Para lograr esto debemos aplicar dos rotaciones: una sobre el eje z y la otra sobre el eje y.

Entonces dado un punto arbitrario en la esfera unitaria, especificado por sus coordenadas terrestres P_e=(lon, lat) se desea llevar este punto al polo norte, es decir se debe mover la tierra hasta que el punto especificado adquiera la posición (0,0,1) en coordenadas rectangulares. Esto cambia la posición de todos los puntos en la superficie de la tierra y el primer problema a resolver es determinar las coordenadas de cada punto de la tierra luego de haber cambiado el polo norte.

El primer problema consiste entonces en que dadas las coordenadas (rectangulares) P_s=(x,y,z) de cualquier punto sobre S²2, se desea obtener las coordenadas (x¢¢, y¢¢, z¢¢) que le corresponden a ese punto luego de rotar la esfera tanto como sea necesario, a fin de que un punto dado arbitrario de coordenadas terrestres P_e=(lon, lat) (longitud y latitud respectivamente) quede en la posición que le correspondía al polo norte (0,0,1).

Se ha dicho "rotar" la esfera porque justamente es eso lo que hay que hacer para llevar el punto elegido al polo norte, el centro de la esfera no cambia de posición y tampoco cambia el tamaño o la forma de la esfera. De hecho para llevar el punto (lon, lat) al polo norte se requiere hacer dos rotaciones en direcciones mutuamente ortogonales: una que lleve el punto sobre el meridiano de Greenwich¹ y otra que lo suba al polo norte.

Como lon es la magnitud del ángulo que forma el punto con el meridiano de Greenwich, entonces la primera rotación debe ser de -lon grados (-[(p)/180] lon radianes) alrededor del eje z, es decir es una rotación del plano xy. Aplicar la rotación es, esencialmente, multiplicar cada vector de la esfera (x,y,z) por la matriz:

æ ç ç ç ç ç è cos(-lonr) - sen(-lonr) 0 sen(-lonr)  cos(-lonr) 0 0 0 1 ö ÷ ÷ ÷ ÷ ÷ ø

(1)

Donde lon_r = [(p)/180] lon.

Usando que sen(-q) = - sen(q) y cos(-q) = cos(q) y multiplicando la matriz 1 por el vector (columna) (x,y) se obtienen las ecuaciones:

x¢ = x cos(lonr) + y sen(lonr) y¢ = y cos(lonr) - x sen(lonr) z¢ = z (2)

El punto (x,y,z), luego de la primera rotación, queda en la posición (x¢, y¢,z¢). Ahora es cuando se debe aplicar la segunda rotación.

Dado que el ángulo que forma el punto original (x,y,z) (y de hecho también (x¢,y¢,z¢)) con el ecuador es lat, para mover el punto al polo norte se debe aplicar una rotación de 90-lat grados alrededor del eje y, es decir, es una rotación del plano xz. La expresión en radianes del ángulo de rotación es: a_r = [(p)/180] (90-lat) y la matriz que expresa dicha rotación es:

æ ç ç ç ç ç è cos(ar) 0 - sen(ar) 0 1 0 sen(ar) 0  cos(ar) ö ÷ ÷ ÷ ÷ ÷ ø

(3)

De donde se obtienen las ecuaciones:

x¢¢ = x¢ cos(ar) - z¢ sen(ar) y¢¢ = y¢ z¢¢ = x¢ sen(ar) + z¢ cos(ar) (4)

Con esto el primer problema queda resuelto. Dado un punto cualquiera que se desea llevar al polo norte P_e=(lon, lat), las coordenadas de cualquier punto sobre la esfera unitaria P_s=(x,y,z) se transforman en las coordenadas (x¢¢, y¢¢,z¢¢) dadas por el sistema de ecuaciones 4. Esto significa, por supuesto que hay que aplicar también el sistema 2, es decir, hacer la composición de las dos transformaciones lineales expresadas por las matrices 1 y 3.

Footnotes:

¹Se ha elegido éste por ser el más sencillo de manipular.