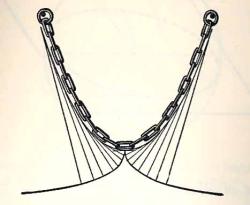
La Catenaria

La curva tractrix está relacionada con otra curva de la que seguramente habrás oído hablar La Catenaria. La curva formada por una cadena uniforme que cuelga libremente se llama Catenaria (del latín catena: cadena).

En tanto que Galileo pensó que la catenaria era una parábola, Huygens, a quien la curva debe su nombre, mostró que es una curva no algebraica, es decir, no hay una ecuación sencilla que la represente. Si se dibujan las líneas tangentes a la catenaria (líneas que apenas la tocan), como en la figura anterior, la curva que es perpendicular a ellas y que toca a la catenaria en su punto más bajo es, precisamente, la tractrix. Se dice que la evoluta de una tractrix es una catenaria. Se observa en la imagen a continuación que, una parábola y una catenaria son muy similares cerca del vértice, no obstante, al aumentar el valor de x (a un valor aproximado de 3 ), la catenaria empieza a rebasar rápidamente a la parábola hasta coincidir nuevamente.

En la figura, la parábola y = x²+1 está en el interior y la catenaria, cuya ecuación es y = ( e^x+e^-x)/2, en el exterior (en azul). Ambas curvas se relacionan cuando la parábola, suponiéndola descansar sobre una mesa, se balancea libremente sobre sus brazos, ya que el foco de la parábola se moverá describiendo la trayectoria de una catenaria.

Nota: En esta dirección encuentras un Java que te permite jugar con la catenaria y sus curvas asociadas: http://www-history.mcs.st-and.ac.uk/history/Java/Catenary.html