Documentación Unidad 1.5 Rectas y ángulos

Mediante construcciones geométricas, determinar las posiciones relativas de dos rectas en el plano y elaborar definiciones de rectas paralelas, perpendiculares y oblicuas.

Establecer relaciones entre los ángulos que se forman al cortarse dos rectas en el plano, reconocer ángulos opuestos por el vértice y ángulos adyacentes.

Instrucciones generales

Los tres botones que se encuentran en la parte derecha tienen la función siguiente:

botones 1

Brinda acceso a la ayuda de las escenas interactivas

Uso de tablas

Para introducir valores es necesario ir dando clic en cada una de las celdas donde se tiene que colocar el resultado, y para comprobar los resultados que introducidos hay que presionar el botón Verificar. Las respuestas correctas aparecerán de color verde y las incorrectas de rojo.

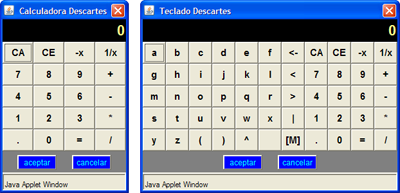
Uso de calculadora

Al hacer doble clic en un campo de texto o en una de las celdas de una tabla aparecerá una calculadora o un teclado virtual.

En ambos casos al terminar de introducir los datos se debe presionar el botón Aceptar; en este momento desaparecerá la calculadora y aparecerá el último resultado escrito en ella.

En caso de escribir una expresión numérica como 2^3+4 al presionar la tecla Intro lo que aparecerá será el resultado de la operación, en este caso 12. El símbolo "^" se utiliza para elevar a una potencia.

1. Rectas

Rectas 1

Las instrucciones de esta escena son las siguientes:

"Rota las rectas y observa que ocurrecon los ángulos que forman

¿Las rectas siempre se intersectan?

¿Pueden ser iguales los cuatro ángulos?"

Es importante señalar que la finalidad de ambas preguntas, es motivar al alumno a responder dichas situaciones. Naturalmente al interactuar con la escena, el alumno obtendrá los elementos necesarios para responder a éstas interrogantes. Por ejemplo para responder si las rectas siempre se intersectan basta con llegar al caso en que son paralelas, en éste caso se despliega un mensaje que indica al usuario que las rectas son paralelas. Si las rectas se intersectan, podemos medir los ángulos formados utilizando el transportador, así podremos ver que los cuatro ángulos formados son iguales entre sí, únicamente cuando son perpendiculares las rectas.

Finalmente en ésta escena se exploran tres tipos de relaciones entre dos rectas en el plano.

La primera es cuando las rectas se intersectan y los ángulos formados no son iguales entre sí. En este caso diremos que las rectas son oblicuas.

La segunda relación que se explora, es cuando las dos rectas se intersectan y los ángulos formados son iguales entre sí. En este caso diremos que las rectas son perpendiculares, y los ángulos son rectos.

La tercera y última es cuando las dos rectas no se intersectan, y por lo tanto no se forma algún ángulo entre ellas. En este caso diremos que las rectas son paralelas.

Sugerencias didácticas

Si las rectas no son paralelas pero tienen inclinación semejante, el punto de intersección puede estar muy lejos del campo visual del pizarrón. Así que aunque parezcan paralelas, el mensaje "Las rectas son oblicuas" nos dice que no lo son.

2. Paralelas

Paralelas 1

El alumno podrá aprender cómo construir una recta paralela a una recta dada y que pase por un punto dado. Lo que tiene que hacer es pulsar uno a uno los botones que aparecen en la parte inferior de la escena, para gradualmente ver los pasos necesarios para obtener la recta deseada. En cada paso, el botón Descripción explica la construcción correspondiente.

Paralelas 2

El objeto de esta escena es que el alumno realice su propia construcción. Las opciones son las mismas que en el caso anterior, pero ahora en cada paso se muestran explicitas las instrucciones correspondientes, con la intención de que el alumno las siga. Así, los únicos objetos geométricos que aparecen son el punto y la recta; los demás serán los que el usuario construya.

Paralelas 3

En esta escena podemos explorar las construcciones ya terminadas, y observar que los trazos geométricos auxiliares no dependen del lugar inicial del punto ni de la recta dada. Por el contrario, como la construcción es dinámica, podemos mover el punto inicial o la recta dada y notar cómo toda la construcción se ajusta y preserva las condiciones constructivas que se dieron a cada objeto geométrico.

Hay que observar que el botón "Ocultar Texto" tiene la función de ocultar las instrucciones del interactivo. Así mismo, el botón "Ocultar Const." tiene la función de ocultar los trazos auxiliares que fueron necesarios para obtener la recta paralela a la recta dada por el punto dado. Esto con el fin de apreciar mejor el objeto geométrico resultante. En cualquier momento podemos recuperar los trazos auxiliares de la construcción.

Finalmente con los botones "Construcción 1" y "Construcción 2", desplegamos las respectivas construcciones propuestas al inicio. Dichas propuestas son dos formas de construir la recta paralela a una recta dada por un punto dado.

3. Perpendiculares

Perpendiculares 1

¿Cómo construir una perpendicular a una recta dada y que además pase por un punto dado? Una manera se muestra en esta escena. Basta oprimir los botones Paso para ver cómo se hace y al apretar Descripción aparece el algoritmo empleado.

Perpendiculares 2

Como en el caso de las paralelas, el objeto de esta escena es que el alumno realice su propia construcción. Las opciones son las mismas que en el caso anterior, pero ahora en cada paso se muestran explicitas las instrucciones correspondientes, con la intención de que el alumno las siga. Los únicos objetos geométricos que aparecen son el punto y la recta.

Perpendiculares 3

Aquí podemos explorar las construcciones ya terminadas y observar que los trazos geométricos auxiliares no dependen del lugar inicial del punto ni de la recta dada. Por el contrario, como la construcción es dinámica, podemos mover el punto inicial o la recta dada y notar cómo toda la construcción se ajusta preservando las condiciones constructivas que inicialmente se le dio a cada objeto.

4. Ángulos

Ángulos 1

Esta escena tiene la dinámica necesaria para comparar los ángulos generados por la intersección de dos rectas. Basta rotar la región donde aparece el pequeño círculo y encimarla en cualquiera de las restantes y decidir cuales ángulos son iguales. El botón Región angular pasa el control a otra de las regiones mientras que Otras rectas proporciona otro ejemplo.

Ángulos 2

En esta última escena se trata de llenar la tabla que aparece a la derecha de la pantalla. Para ello se cuenta con un transportador, que puede activarse presionando el botón amarillo donde aparece su imagen en pequeño.

Dicho transportador tiene un recurso extra que permite visualizar numéricamente el ángulo medido.

Los botones hacen lo que dicen: Verificar la respuesta, Resolver la pregunta y pasar a Otro ejercicio.

Sugerencias Didácticas

En la escena inicial hacer la observación de que los cuatro ángulos formados en dicha intersección son iguales solamente cuando las rectas son perpendiculares. En caso contrario, cada ángulo será igual únicamente a su opuesto por el vértice.

En la segunda escena se recomienda efectuar todas las mediciones que sean necesarias para familiarizarse con el uso del transportador, así como justificar o corregir las observaciones de los alumnos.

Posteriormente, se sugiere restringir al mínimo el uso del transportador, esto es, intentar deducir las medidas de los ángulos a partir de pocas mediciones iniciales.

Por ejemplo, si en la intersección de dos rectas uno de los cuatro ángulos mide 35°, ¿cuánto mide un ángulo adyacente al de 35°?.

Los ángulos opuestos son iguales entre sí, y si uno de los cuatro mide 35° significa que su opuesto también mide 35°, que sumados nos da 70°. Pero los otros dos ángulos también son iguales entre sí, por ser opuestos, y como 70° es la diferencia entre 360° y 290°, se tiene que el ángulo adyacente buscado mide exactamente la mitad de 290°, o sea 145°.

Unidad 1.5

Rectas y ángulos

RES

Propósito