
Unidad 2.1
Jerarquía de operaciones y uso de paréntesis
RES
Propósito
Que el alumno comprenda la jerarquía de los signos de operación y el uso adecuado de los paréntesis.
Instrucciones generales
La unidad se divide en cuatro apartados :
2. Dos operaciones
3. Tres operaciones
4. Paréntesis
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
![]()
Los tres botones que se encuentran en la parte derecha tienen la función siguiente:
 Brinda acceso a la ayuda de las escenas interactivas
Brinda acceso a la ayuda de las escenas interactivas
 Herramientas de Enciclomedia
Herramientas de Enciclomedia
 Cerrar la ventana
Cerrar la ventana
1. Claudia y Juan
Este apartado consta de dos escenas, las cuales son un primer acercamiento a la jerarquía de operaciones. En la primera se le cuestiona al alumno cual de los dos ejercicios presentados es correcto. En la segunda se le pide resolver dieciséis ejercicios que combinan los cuatro operadores: +, -, x y ÷.
Claudia y Juan 1
Como se muestra en la escena, Claudia y Juan obtuvieron resultados distintos al efectuar las mismas operaciones. ¿Por qué?
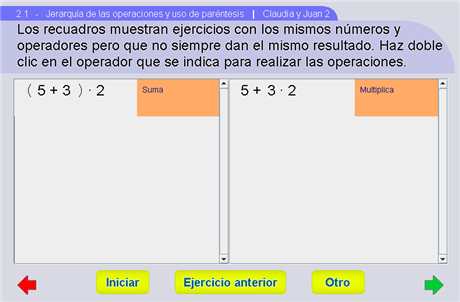
Claudia y Juan 2
Así como en la escena anterior, se presenta un mismo ejercicio que deben resolver, pero en este caso el alumno deberá seguir las instrucciones que cada recuadro tiene. El botón Iniciar hace que aparezca nuevamente el ejemplo con que se trabajaba; Ejercicio anterior nos lleva al último que se vio y Otro conduce al siguiente ejercicio. Esto ocurre, al mismo tiempo, en ambos recuadros.
Sugerencias didácticas
A través de algunos ejemplos se espera que los alumnos observen y tal vez puedan determinar la jerarquía de las operaciones. Se le recomienda al profesor cuestionarle al alumno cada ejemplo que va apareciendo antes de continuar con el siguiente ejercicio. A continuación planteamos algunas preguntas que el profesor puede hacerle al alumno.
Debemos dejar claro que los resultados que obtienen Claudia y Juan en algunos casos serán iguales. Es decir, si le damos clic a cualquiera de los dos botones, el resultado será correcto.
Si en el ejercicio que hacen Claudia y Juan, los resultados son los mismos, entonces se les preguntará a los alumnos: ¿Qué operadores se están involucrando?, ¿Los resultados serán iguales siempre que se utilice esta combinación de operadores?, ¿Si esto no es cierto, entonces cuál es la razón de este resultado?, ¿Si es cierto, entonces que podemos concluir?
Ahora, cuando el resultado es diferente se les puede preguntar: ¿Quién tiene la respuesta correcta según ustedes?, ¿Por qué?, ¿Qué se puede decir de todos los ejemplos construidos con estos operadores? Para contestar esta última pregunta el profesor puede motivar al alumno a realizar más ejercicios en un papel, que involucren los mismos operadores para construir la regla correspondiente.
2)Claudia y Juan 2Ya que hicieron el análisis anterior, en esta escena pueden aclarar, en que casos, los resultados de las operaciones son iguales o diferentes. Para ello, se recomienda que después de realizar los ejercicios, hagan una lista de las combinaciones de los operadores en los que ocurre que los resultados son siempre iguales. Debemos mencionar que en esta lista de 16 ejercicios propuestos, los resultados serán iguales sólo en los últimos 4. Incluso, se le debe preguntar al alumno, si en estos cuatro casos siempre ocurrirá lo mismo.
Además, esta escena nos ayudará a encontrar el orden correcto para resolver las operaciones. Se pueden revisar ejercicio por ejercicio y mencionar que operador debe resolverse primero y porqué. De esta forma, se les puede pedir a los alumnos que escriban en sus cuadernos la jerarquía de las operaciones.
2. Dos operaciones
Este apartado consta de una escena con quince ejercicios que combinan los cuatro operadores: +, -, x y ÷. Por ejemplo: (+ y -) ó (x y ÷).
El alumno deberá resolver los ejercicios modificando los operadores en el recuadro izquierdo. Del lado derecho de este recuadro aparecerá la instrucción a seguir, por ejemplo, si dice "Suma" hay que colocar el ratón sobre el operador "+" y dar doble clic sobre él. Al mismo tiempo de resolver el ejercicio, se va a ir modificando el árbol que se encuentra del lado derecho de la escena. Obsérvese que la última rama es la operación que se está pidiendo resolver primero. Los botones Iniciar, Ejercicio anterior y Otro tienen la misma función que en la escena de Claudia y Juan 2.

Sugerencias didácticas
Es muy importante que cuando se está resolviendo el ejercicio, el profesor haga notar lo que va ocurriendo en el árbol derecho. Para explicarlo se debe decir que el operador que se está pidiendo resolver primero es aquél que está en la última rama del árbol. El resultado que queda entonces es con un solo operador, por lo que su solución ya es conocida. Así, se puede mencionar que el árbol funciona como una ayuda para resolver cualquier ejercicio de dos operadores: se observa el árbol, se identifica la última rama que tiene y se resuelve la operación.
Se recomienda que el alumno realice por lo menos los quince ejercicios propuestos.
3. Tres operaciones
Este apartado consta también de una escena pero con nueve ejercicios que combinan los cuatro operadores.
El alumno deberá resolver los ejercicios propuestos con tres operadores en el recuadro izquierdo, siguiendo las instrucciones que se presentan y escribiendo directamente los resultados de lo que se te va indicando. Al mismo tiempo de resolver el ejercicio, se va a ir modificando el árbol que se encuentra del lado derecho de la escena. Como mencionamos en el apartado Dos Operaciones , la primera operación que se va a realizar es exactamente la última rama del árbol. Los botones Iniciar, Ejercicio anterior y Otro funcionan como antes.

Sugerencias didácticas
Es muy importante que cuando se está resolviendo el ejercicio, el profesor haga notar lo que va ocurriendo
en el árbol derecho. Para explicarlo se debe decir que el operador que se está pidiendo resolver primero es aquél
que está en la última rama del árbol.
Sin embargo, en esta escena el árbol tendrá más ramas: izquierdas y derechas y, es probable
que en algunos casos se tengan ramas en el mismo nivel. Esto significa que si se tienen las combinaciones de operadores: (+ y -) ó (x y ÷), en el mismo nivel,
la solución se debe obtener escribiendo el resultado de cualquiera de los operadores.
Se recomienda discutir los nueve ejercicios propuestos, en especial los casos en que se tengan ramas en el mismo nivel. Que los alumnos hagan las repeticiones necesarias y los valores hasta que obtengan experiencia en la solución de este tipo de ejercicios.
4. Paréntesis
Este apartado consta de solamente una escena, la cual consta de ejercicios que combinan los cuatro operadores.
Aquí se trata de que el alumno mueva apropiadamente los paréntesis hasta obtener la posición apropiada y por tanto el resultado correcto.

Sugerencias didácticas
El profesor debe explicar que dentro de la jerarquía de operaciones, el paréntesis siempre se resuelve primero, como lo vimos en las escenas anteriores. Sin embargo, en esas escenas el paréntesis únicamente nos ayudaba a elegir el operador adecuado. En este apartado se enfatiza su importancia para romper la jerarquía de las operaciones.
El profesor puede plantear varios ejercicios que contengan tanto al paréntesis como a los cuatro operadores, para que el alumno practique lo aprendido en esta unidad.
Créditos
Autora
Alexandra Guzmán Velázquez
Colaboraciones
Julio César Domínguez Tovar ayudó a mejorar la funcionalidad de la escena "Claudia y Juan".
Agradecimientos
A María Teresa Rojano Ceballos por sus sugerencias didácticas.
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes.
Como la unidad utiliza el applet Descartes, propiedad del Ministerio de Educación de España,
sus contenidos se distribuyen bajo una licencia de
