Unidad 2.3
Cubos, prismas y pirámides
RES
Propósito
Que el alumno comprenda las características de cubos, prismas y pirámides. Que construya desarrollos planos de cubos, prismas y pirámides rectos. Que anticipe diferentes vistas de un cuerpo geométrico.
Instrucciones Generales
Esta unidad contiene cinco apartados:
1. Desarrollos
2. Armados
3. Ejercicio 1
4. Ejercicio 2
5. Vistas

Los tres botones que se encuentran en la parte
derecha tienen la función siguiente:
 Brinda acceso a la ayuda de las escenas interactivas
Brinda acceso a la ayuda de las escenas interactivas
 Herramientas de
Enciclomedia
Herramientas de
Enciclomedia
 Cerrar la ventana
Cerrar la ventana
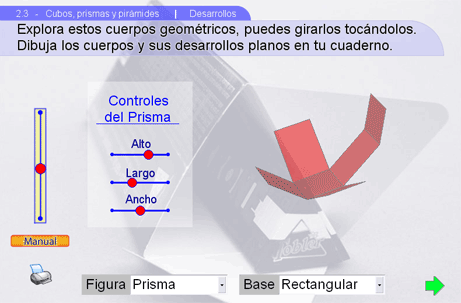
1. Desarrollos
Este apartado permite ver cómo se construyen algunas figuras geométricas ya sea prismas, pirámides y los sólidos platónicos mediante sus desarrollos planos.
Instrucciones
Usa el menú Figura para seleccionar algún cuerpo geométrico del que se desea ver uno de sus posibles desarrollos planos.
En los casos de Prismas y Pirámides se puede:
- Modificar las medidas de la altura y la base
- Escoger la forma de la base ya sea rectangular, pentagonal o hexagonal
- Si se escoge base rectangular, se puede modificar el ancho y largo de las caras
El botón de la impresora muestra varios desarrollos planos para imprimir y posteriormente recortar y armar.
Sugerencias Didácticas
El apartado está diseñado para aumentar la percepción espacial de los alumnos al permitirles ver en pantalla imágenes, las cuales posteriormente dispararán su imaginación. Para la presentación de esta escena, es conveniente pedirles a los alumnos que reproduzcan en papel algunos desarrollos planos, los que pueden imprimirse usando el botón donde aparece la impresora.
Algunas cosas que es conveniente hacer notar es el número de vértices, aristas y caras que tiene cada figura. Pueden hacerse las siguientes preguntas:
- ¿Cuántas
caras tienen cada prisma, cada pirámide, el cubo, el octaedro,
etc.?
Respuesta: Ver tabla más abajo. - ¿Y aristas?
R: Ver tabla más abajo. - ¿Cuántas
caras tocan un vértice?
R: Ver tabla más abajo. - ¿Cuántos
vértices (esquinas) hay en cada cara?
R: Ver tabla más abajo y en especial discutir el caso de la pirámide. -
Un poliedro se dice que es de vértices uniformes si en cada vértice hay el mismo número de caras ¿Cuáles figuras de las que aquí se presentan son regulares?
R: Por ejemplo, el cubo tiene 3 caras en cada esquina (vértice); pero, en la pirámide con base cuadrada, el vértice de la punta tiene 4 caras, mientras los vértices de la base solo tienen 3. Puede verse que todos los poliedros que se presentan, salvo la pirámide, son de vértices uniformes. - Usando la
pregunta anterior ¿habrá vértices en algún
poliedro que solo tengan 2 caras?
R: La respuesta esperada es que no, ya que, para tener menos de 3 caras, el vértice tendría que estar en una figura plana, donde, por consecuencia, solo hay una cara. - ¿Se
podrá hacer una figura con puros hexágonos?
R: No, ya que los hexágonos cubren el plano y no permiten hacer 2 dobleces que formen un ángulo (este tema se abordará en profundidad en la unidad de "Cubrimientos del Plano", y es de gran utilidad presentar ideas como ésta para ir preparando a los alumnos).
-
La siguiente pregunta es muy interesante y su respuesta ha sorprendido a muchísima gente a través de los últimos 3 siglos.
En un cubo, ¿cuánto suma el número de vértices más el de caras menos el número de aristas?, es decir Vértices + Caras – Aristas = ?
¿Y en los casos de pirámide o tetraedro? ¿Y que sucede con el octaedro o icosaedro? R: En todos estos cuerpos geométricos que hemos visto, la respuesta es 2. Al resultado de la operación "Vértices + Caras – Aristas" se le llama característica de Euler (Pronúnciese "Oiler") y es de gran utilidad en el estudio de la geometría avanzada. Se han hecho muchísimos estudios con respecto a esta característica, por ejemplo, si el poliedro no tiene hoyos, entonces esta característica es 2, pero si tiene un hoyo, como por ejemplo en una dona poligonal (abajo aparece una dona pentagonal con corte cuadrado), su característica de Euler es 0. ¿Qué pasará con figuras con más agujeros?

|
Figuras
|
Vértices
|
Aristas
|
Caras
|
Caras
por vértice |
Vértices
por cara |
| Prisma rectangular |
8
|
12
|
6
|
3
|
4
|
| Prisma pentagonal |
10
|
15
|
7
|
3
|
4 ó 5
|
| Prisma hexagonal |
12
|
18
|
8
|
3
|
4 ó 6
|
| Pirámide rectangular |
5
|
8
|
5
|
3 ó 4
|
3 ó 4
|
| Pirámide pentagonal |
6
|
10
|
6
|
3 ó 5
|
3 ó 5
|
| Pirámide hexagonal |
7
|
12
|
7
|
3 ó 6
|
3 ó 6
|
| Tetraedro |
4
|
6
|
4
|
3
|
3
|
| Cubo |
8
|
12
|
6
|
3
|
4
|
| Octaedro |
6
|
12
|
8
|
4
|
3
|
| Dodecaedro |
20
|
30
|
12
|
3
|
5
|
| Icosaedro |
12
|
30
|
20
|
5
|
3
|
| Dona pentagonal (Arriba) |
24
|
48
|
24
|
4
|
4
|
Presionando la flecha verde se pasa a la escena siguiente donde los alumnos pueden experimentar con algunos desarrollos planos.
Nota: El concepto de cuerpo geométrico y de poliedro se usan de forma indistinta en esta documentación, aunque es conveniente aclarar que un cuerpo geométrico puede no tener caras, aristas y vértices, como por ejemplo las esferas.
2. Armado
En este apartado podemos construir todos los desarrollos planos que generan el mismo cuerpo y ver cómo se doblan éstos. La figura en cuestión es un tetraedro, o sea una pirámide triangular con caras equiláteras.
Instrucciones
En el lado derecho aparece el desarrollo plano de un tetraedro, el cual podemos modificar arrastrando las caras que lo forman. Las caras se trasladan arrastrando los círculos blancos que tienen en su interior. Al tocar uno de estos círculos, la cara correspondiente se selecciona y se acentúan los colores de sus aristas mostrando dónde va pegada cada cara. Una vez que una cara está en movimiento, ésta solo se pegará al desarrollo plano, en las aristas coloreadas.

Sugerencias Didácticas
Esta escena está diseñada para que los alumnos descubran todos los desarrollos planos que forman un tetraedro. Sólo son 2, los cuales se pueden encontrar varias veces rotados o trasladados al explorar la escena. Sugiera a los alumnos que traten de argumentar por que no existen más desarrollos planos. Una posible respuesta a este hecho es que si se colocan los cuatro triángulos tocando un vértice, al doblarse la figura nos queda una pirámide de 4 caras sin base alguna. Fuera de esta no hay más opciones.

Obsérvese que en el fondo de la escena se ve una flor que cumple con las propiedades de armado del tetraedro aquí expuesto.
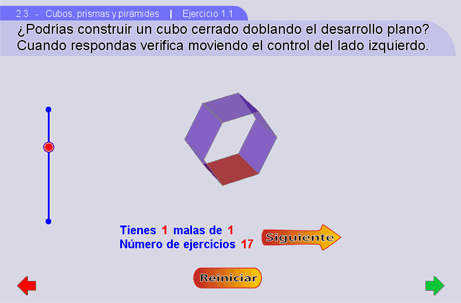
3. Ejercicio 1
Este
apartado evalúa a los alumnos
haciéndolos identificar cuándo tenemos un desarrollo
plano verdadero de un cubo o pirámide y cuándo no.
En él, se
presentan diferentes desarrollos planos del cubo y de la
pirámide hexagonal, algunos son verdaderos y otros, por encimar
o faltar caras, son desarrollos falsos.
Menú
El apartado comienza con la escena
Menú. En esta escena se ven dos botones, mediante los cuales se
selecciona la figura con la que se realizará el ejercicio.
Instrucciones
Generales
Al oprimir el botón "comenzar" aparecerán dos botones y un desarrollo plano. Después de analizar detenidamente la figura, si se considera que el desarrollo es verdadero, presione el botón "si", y si se cree que es falso, presione "no". Al hacer esta pulsación, automáticamente aparecerá una paloma o un tache, dependiendo de la veracidad de su respuesta y se animará el armado correcto o incorrecto del cubo (o pirámide) según sea el caso. Del lado izquierdo aparecerá un control en barra con el que es posible modificar la apretura de la figura. Este control es muy útil en el caso de que haya quedado alguna duda sobre que cara se encima con que otra (en los desarrollos falsos).
En la parte inferior aparecerá un botón que dice "Siguiente" con el que se continua el ejercicio con otro desarrollo.
Junto a los botones de "Si" y "No" se indica, con números rojos, el índice del ejercicio en el que va y el número de errores.
Al finalizar el total de ejercicios aparecerá un marcador de aciertos y errores acompañado de un mensaje que puede ir desde un "Excelente" hasta un amable "Hay que repasar más".
Sugerencias Didácticas
Esta escena puede utilizarse para evaluar alumnos de manera individual o en equipos.
Se sugiere la participación de los alumnos dando sus respuestas (si o no) y argumentando brevemente al resto de los compañeros.
4. Ejercicio 2
En este apartado los alumnos deben identificar cuales caras de un cubo o de una pirámide van unidas entre sí. Para esto deben visualizar mentalmente en que lugar se deberá pegar alguna arista particular.
Menú
El apartado comienza con la escena Menú. En esta escena se ven dos botones, mediante los cuales se selecciona la figura con la que se realizará el ejercicio.
Instrucciones Generales
Una vez seleccionada la figura en el Menú se presentan desarrollos planos de la figura y se pide que relacionar las caras arrastrando un punto rojo. El objetivo es relacionar la cara donde aparece el punto rojo, con la cara correspondiente de pegado.
Del
lado izquierdo aparece el desarrollo plano en tres dimensiones, al
pulsar el botón de "Ayuda" se anima el doblado del desarrollo.
Solo se puede utilizar este botón un numero determinado de veces
por lo que se recomienda no abusar de el.
En la parte central aparecen el número de aciertos, el número de ejercicio en el que se va, el total y la cantidad de Ayudas disponibles.

Sugerencias Didácticas
Al igual que la escena anterior, esta escena puede utilizarse para evaluar alumnos de manera individual o en equipos.
Se sugiere no utilizar la ayuda a menos que sea estrictamente necesario, con el fin de fomentar la imaginación espacial.
5. Vistas
Este apartado se divide en dos escenas: una exploratoria y otra de ejercicios.
Vistas 1
La primera nos permite apreciar, desde diferentes ángulos, algunos conjuntos de cubos apilados. La idea es que los alumnos entiendan cuales son las vistas frontal, lateral y superior del mismo conjunto.
Obsérvese que las vistas se colorean de azul, amarillo o verde, colores que corresponden al cuerpo geométrico formado por cubos.
Presionando el menú de ejemplos se observan diferentes cuerpos con sus respectivas vistas.
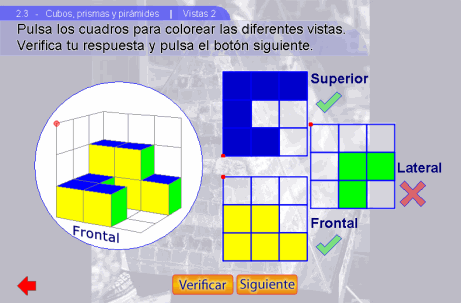
Vistas 2
En Vistas 2 las retículas aparecen vacías, y al pulsar sobre alguna casilla, ésta se iluminan. El objetivo es que los alumnos puedan dibujar correctamente las tres proyecciones, Frontal, Superior y Lateral. Como ayuda para entender la posición de la vista y de la proyección, aparece un punto rojo.
Una vez iluminadas las vistas, el botón Verificar califica las respuestas, ya sea con una paloma o con un tache.
Sugerencias Didácticas
Esta escena está diseñada para hacer trabajar la imaginación de los alumnos, haciéndolos visualizar en sus mentes las diferentes vistas de un cuerpo geométrico simple. Se sugiere incitar a los alumnos a dibujar en sus cuadernos cuerpos geométricos hechos con cubos como los aquí presentados. Comience con más de 5 cubos y vaya elevando el número hasta que utilicen más de 32. Parece elevado el numero, pero en realidad no lo es tanto por utilizar largo, ancho y alto. Pídales que hagan sillas, mesas, sofás, automóviles, televisores, mochilas, sombreros, naves espaciales, etc. con cubos y luego que dibujen sus diferentes vistas. Júntelos en equipos y que se muestren sus dibujos comentándolos entre ellos. Puede hacerse un concurso para ver el cuerpo geométrico más artístico u original.
Datos curiosos sobre los desarrollos planos:
- Los desarrollos planos son de gran utilidad en el doblado de objetos, por ejemplo, para crear materiales para empaques como cajas, recipientes, contenedores, etcétera.
- ¿Cuál es el objeto geométrico, con volumen fijo, que puede apilarse sin dejar huecos y que usa la menor cantidad de material en su desarrollo plano? Dicho de otra manera, ¿Qué objeto cubre el espacio o sea, lo tecela1 de la manera más eficiente? Actualmente (junio 2007) no se sabe. Quién lo descubra seguramente recibirá algo más que fama inmortal.
- Para ahorrar espacio, en la ingeniería espacial se transportan los cuerpos geométricos en forma de desarrollos planos, los cuales se desdoblan y pliegan formando cúpulas, receptores de energía solar y antenas, entre otras cosas.
- Desde hace más de 2500 años las culturas japonesa y china han favorecido el juego del doblado de papel. Al doblarlo obtenían cuerpos geométricos semejantes a figuras de la naturaleza o de la vida cotidiana. El nombre japonés de este arte es “Origami”. Donde Oru es plegar y Gami, papel.
- Cuando Marco Polo (Siglo XIII) regresó de sus viajes a Oriente, en particular a China, trajo consigo habitantes de aquellos parajes, los cuales cultivaron en Europa este mismo arte. La única diferencia fue que le llamaron Papiroflexia. El mayor desarrollo europeo en esta actividad se dio en España.
(1) El cubo es un ejemplo de estos cuerpos que, al apilarlo a lo largo y a lo ancho, cubre el espacio. Las pirámides en general no tienen esta propiedad. Si se hace una comparación con las figuras del plano este hecho resulta curioso, ya que los cuadrados y los triángulos si llenan el plano (esto se verá con más detalle en la unidad "Cubrimientos del plano").
Créditos
Autor
Claudio Francisco Nebbia Rubio
Agradecimientos
A Carlos Alberto Serrato
Hernández , a Oscar Escamilla González y a Erika Paulina
Tovilla Quesada, integrantes del Grupo Descartes, por colaborar
ampliamente con sus ideas y apoyo en la realización de esta
unidad.
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes.
Como la unidad utiliza el applet Descartes, propiedad del Ministerio de Educación de España,
sus contenidos se distribuyen bajo una licencia de
