Unidad 2.4Volumen de cubos, prismas y pirámidesRESPropósitoQue el alumno comprenda diferentes aproximaciones a la fórmula para calcular volúmenes de prismas. Así mismo, que vea como surge la fórmula para calcular volúmenes de pirámides. Por último, que tenga un acercamiento a la idea de límite y de estimación de volúmenes. Instrucciones GeneralesEsta unidad contiene cinco apartados: 1. Prismas 1
Los tres botones que
se encuentran en la parte derecha tienen la función siguiente:
Nota: Los apartados Prismas 1, 2 y 3 están diseñados para llevar al usuario a través de diferentes ideas que permiten generar, poco a poco, el concepto de volumen de prismas. Véanse estas secuencias en el orden propuesto ya que están seriadas.
1. Prismas 1El apartado Prismas 1 enseña a profundidad como calcular el volumen de prismas con medidas enteras, haciendo que el alumno comprenda el uso de las multiplicaciones para dicho propósito, sustituyendo así, el conteo de cubos (uno por uno) que caben en el interior.
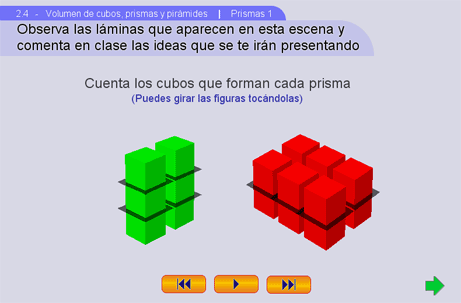
Prismas 1-1 Presentación de las ideas principales: dividir el prisma en cubos unitarios Los controles para controlar la presentación aparecen en la parte inferior de la escena y son:
Advertencia: La escena se puede pausar de forma automática en momentos clave, por ejemplo, cuando se plantea una pregunta que haya que responderse. Sugerencias DidácticasAunque la escena es prácticamente autocontenida se sugiere lo siguiente: En la escena aparecen las siguientes preguntas abiertas. A continuación presentamos algunas posibles respuestas y observaciones:
2. PruebaEsta escena consta
de 3 ejercicios que se acceden desde un menú principal los
cuales están dedicados a ejercitar lo aprendido. Cada escena
contiene un entretenido juego que mide la habilidad para aplicar los conocimientos
enseñados y la velocidad de uso de los mismos. El objetivo de
cada juego es contar el número de cubos en los que se divide un
prisma o una figura irregular, para lograr un buen tiempo hay que
utilizar la fórmula de lado por lado por lado. En el tercer ejercicio, no es posible dadas las características de las
figuras.
Prueba Menú Aquí
se observa un menú con 3 botones: Prueba 1, Prueba 2 y Prueba 3. Con cada uno de ellos se puede acceder a uno de los ejercicios, los
cuales están graduados por dificultades.
En este ejercicio aparece un prisma en su
vista isométrica la cual permite un rápido conteo de las
dimensiones del cubo. Al terminar el conteo hay que escribirlo
en el espacio, el cual, en el
caso de utilizar el teclado, se actualiza con la tecla Intro.
Utilizando el pizarrón electrónico se puede acceder a una
calculadora pulsando
dos veces sobre el espacio para anotar el resultado. Cada serie
tiene 10 ejercicios. En este ejercicio aparece un prisma en su
vista tridimensional la cual dificulta un rápido conteo
de las dimensiones del cubo. Al terminar el conteo hay que
escribirlo en el espacio, el cual, en el caso de utilizar el
teclado, se actualiza con la tecla Intro. Utilizando el
pizarrón electrónico se puede acceder a una calculadora pulsando dos veces
sobre el espacio para anotar el resultado. Cada serie tiene 10
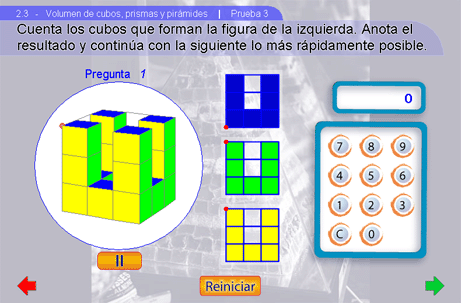
ejercicios. En este ejercicio aparecen figuras
irregulares hechas con cubos. Al terminar de contar el número de
cubos que forman cada figura hay que escribirlo utilizando el
teclado numérico que aparece del lado derecho. Si se comete algún error, puede corregirse
con la tecla "C" del mismo teclado. Cada serie tiene 10
ejercicios. Formar
equipos de 5 alumnos y hacer competencias para ver cual obtiene un
mejor tiempo. Estas escenas pueden utilizarse para evaluar a los
alumnos en grupo o de forma individual. Presionando
la flecha verde se pasa
a la escena siguiente. El
apartado Prismas 2 complementa al anterior
introduciendo, además de las medidas enteras, medidas
fraccionarias y decimales. En el se presenta una aproximación
completamente diferente a la fórmula de volumen a través de
proporciones, enriqueciendo de esta forma, las perspectivas que tiene el
alumno del mismo concepto. Este
apartado se divide en 2 escenas teóricas Prismas 2-1
está dedicada a mostrar el problema de aplicar el conteo de
cubos en prismas con medidas no enteras (motivación), y Prismas
2-2 que presenta una idea alterna para deducir la fórmula
del volumen de prismas
mediante proporcionalidad (Idea que se utilizará también
posteriormente en el apartado Prismas 3). Los
controles para controlar la presentación aparecen en la parte
inferior de la escena y son: Advertencia: La escena se puede pausar de
forma automática en momentos clave, por ejemplo, cuando se
plantea una pregunta que hay que responder. Aunque
la escena es prácticamente autocontenida se sugiere lo siguiente: Prismas 2-2 Los
controles para controlar la presentación aparecen en la parte
inferior de la escena y son: Advertencia: La escena se puede pausar de
forma automática en momentos clave, por ejemplo, cuando se
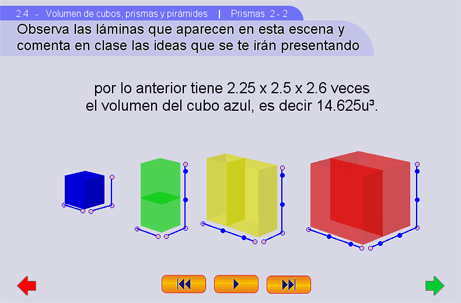
plantea una pregunta que hay que responder. En Prismas
2-2, en algunas láminas, aparecen preguntas que se
responden
inmediatamente en la siguiente lámina, la discusión
completa se
puede realizar terminando la escena. Hágase hincapié en
que con
las ideas presentadas, utilizando el concepto de proporción se
logra demostrar que,
la fórmula obtenida en el apartado 1, sirve aquí también. El
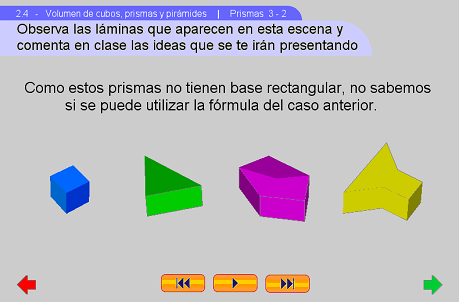
apartado Prismas 3 generaliza lo más posible
(en este nivel medio) el concepto de volumen en prismas, considerando
éstos con bases no rectangulares. Para ello se introducen ideas que, mediante un
primitivo concepto de límite, permiten aproximarse al
cálculo y/o estimación del área de la base de
diferentes prismas. Prismas 3-1 Al comenzar la escena se
presentará una animación explicando como se puede deducir
fácilmente la fórmula para calcular el volumen de
pirámides con base triangular. Al finalizar la animación
se muestra un prisma con base triangular editable, el cual está
encerrado en un prisma rectangular apropiado para comprender las ideas
expuestas durante la presentación. Prismas
3-2 Los
controles para controlar las presentaciones aparecen en la parte
inferior de las escenas y son: Conviene advertir
que las escenas se pausan de forma automática en momentos clave,
por ejemplo, cuando se plantea una pregunta que hay que responder. Aunque
la escena es prácticamente autocontenida se sugiere lo siguiente:
Aunque
la escena es prácticamente autocontenida se sugiere hacer las
siguientes preguntas: Prismas
3-3 Los
controles para controlar las presentaciones aparecen en la parte
inferior de las escenas y son: Conviene advertir
que las escenas se pausan de forma automática en momentos clave,
por ejemplo, cuando se plantea una pregunta que hay que responder. Aunque
la escena es prácticamente autocontenida se sugiere lo siguiente: En Prismas 3-2
aparecen las siguientes frases o preguntas que presentamos a
continuación con algunas posibles respuestas y observaciones: El
apartado Pirámides presenta al alumno, una
argumento riguroso de porque el volumen de una pirámide es un
tercio del volumen de un prisma con igual base y altura. Para ello se
presentan conceptos e ideas claves en el estudio de la geometría
contemporánea de forma clara y accesible para los estudiantes de
nivel secundaria; por ejemplo, las ideas de Cavalieri para calcular
volúmenes se aplican para calcular el volumen de
pirámides
deformadas. Este
apartado expone, con una presentación, como se obtiene la
fórmula para calcular el volumen de las pirámides de las cuales
conocemos el área de sus bases y la altura. En total son
2 escenas, las cuales son de
carácter teórico. En la primera Pirámides 1 se
presenta la motivación, mostrando que no es posible meter cubos
enteros que llenen una pirámide cualquiera. En Pirámides
2 se explica de
forma interactiva por que dos pirámides con la misma base y con
la
misma altura tienen el mismo volumen. Pirámide 1 Los
controles para controlar las presentaciones aparecen en la parte
inferior de las escenas y son: Conviene advertir
que las escenas se pausan de forma automática en momentos clave,
por ejemplo, cuando se plantea una pregunta que hay que responder. Aunque
la escena es prácticamente autocontenida se sugiere lo siguiente: En Pirámides
1 aparecen las siguientes preguntas que presentamos a
continuación con algunas posibles respuestas y observaciones:
Pirámide 2 Los
controles para controlar las presentaciones aparecen en la parte
inferior de las escenas y son: Hay varios controles extras que irán apareciendo
durante la presentación, su explicación se detalla en la
propia escena. Conviene advertir
que las escenas se pausan de forma automática en momentos clave,
por ejemplo, cuando se plantea una pregunta que hay que responder. En Pirámides
2 aparecen una gran cantidad de afirmaciones y preguntas que no es
importante responder. Los métodos que aquí se presentan
son propios de estudios superiores y solo se muestran a modo de
demostración para motivar a los alumnos a seguir trabajando con
las matemáticas y que no crean que todo está terminado en
este punto. El
apartado Ejercicios está inspirado en el
trabajo del matemático alemán Hans Freudenthal
sobre la experiencia del niño
al aprender el concepto de volumen. La conservación de volúmenes y
capacidades bajo ciertas deformaciones de un envase favorece el
entendimiento general de los conceptos. En esta unidad se muestran
diferentes recipientes con formas diversas para ser llenados con el
contenido de un prisma. Se sugiere comenzar con este último apartado en caso
de contar con suficiente tiempo para presentar este tema. El
punto blanco que se encuentra del lado derecho del frasco derecho
controla el nivel al que se predice que va a llegar el agua
después de hacer el trasvase. Muévase arriba y abajo para
ver como el nivel rojo cambia de lugar. El
botón verificar, realiza el trasvase de forma animada. El
botón siguiente cambia de frasco. La
escena está creada para fomentar la experiencia del volumen en el
alumno, se sugiere por lo tanto, hacer participar a los alumnos
haciendo equipos. Un representante de cada equipo pone una marca
utilizando las herramientas, en donde cree que va a llegar el nivel de
agua y gana el equipo que se acerque más. Dada una
esfera de radio 1 es posible partirla en un numero finito de pedazos
que al moverlos (trasladando y rotando) pueden forman 2 esferas del
mismo radio. Esto afecta a la intuición que considera imposible tal afirmación.
¿Cómo un objeto que tiene determinado volumen puede
partirse en pedazos y armarse de nuevo un objeto con 2 veces el
volumen anterior? Este resultado se produce gracias a que no a
todos los cuerpos en el espacio (no todos los conjuntos) se les puede calcular el volumen. Para
que este resultado sea cierto
es necesario considerar el axioma
de elección que ha causado grandes polémicas en la
comunidad matemática y no es completamente aceptado actualmente.
Autor |
Brinda acceso a
la ayuda de las escenas interactivas
Herramientas
de Enciclomedia
Cerrar 
