Documentación Unidad 3.2 - Resolución de ecuaciones de primer grado

Utilizar el modelo de la balanza como un apoyo concreto para dar sentido a las propiedades de la igualdad en la solución de ecuaciones.

Instrucciones generales

Esta unidad fue diseñada para ayudar a los alumnos a resolver ecuaciones lineales con ayuda del modelo de la balanza. La primera parte (Balanza) es una balanza simple en la que se pueden resolver ecuaciones que tengan sólo números positivos. La segunda parte es una balanza más interesante en donde se pueden representar y resolver ecuaciones con números positivos y negativos. En principio, el modelo de la balanza ayuda a visualizar el proceso de resolver una ecuación lineal: "lo que se haga de un lado se hace del otro". En este modelo la igualdad equivale al equilibrio. Despejar la x equivale a dejar una pesa x sola en un lado de la balanza. Entonces es importante que constantemente se esté diciendo esto a los alumnos para que después, ya sin la balanza, puedan usar ese método para resolver más ecuaciones usando números fraccionarios, decimales, etc.

Los tres botones que se encuentran en la parte derecha tienen la función siguiente:

botones 1

Brinda acceso a la ayuda de las escenas interactivas

Uso de campos de texto

En algunas escenas aparecen campos de texto para que el usuario escriba en ellos valores o expresiones numéricas. La forma de uso de estos campos es la siguiente:

Uso de tablas

Para introducir valores es necesario ir dando clic en cada una de las celdas donde se tiene que colocar el resultado, y para comprobar los resultados introducidos hay que presionar el botón Verificar. Las respuestas correctas aparecerán en color verde y las incorrectas en rojo.

Uso de calculadora

Al hacer doble clic en un campo de texto o en una de las celdas de una tabla aparecerá una calculadora o un teclado virtual.

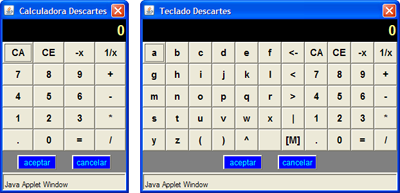
En ambos casos al terminar de introducir los datos se debe presionar el botón Aceptar; en este momento desaparecerá la calculadora y aparecerá el último resultado escrito en ella.

1. Balanza

Balanza 1

Está diseñada para que los alumnos se familiaricen con la balanza. Para esto, el objetivo de esta escena es simplemente encontrar cuánto pesa x poniendo pesas de peso 1 del lado derecho de la balanza hasta que ésta se equilibre. Se espera que el alumno llegue por sí solo a la equivalencia equilibrio-igualdad. Si le sobra o estorba alguna pesa, puede echarla a cualquiera de los botes de basura.

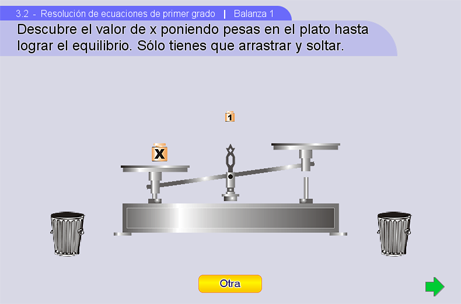
Note la flecha verde abajo a la derecha en la imagen de arriba. Sirve para acceder a la siguiente escena, que es:

Balanza 2

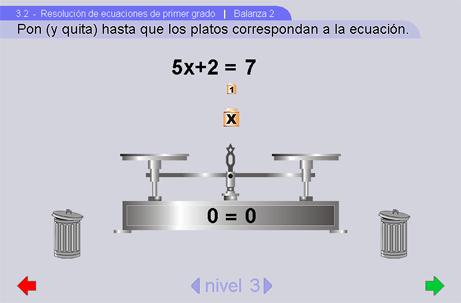
La balanza 2 fue diseñada para que los alumnos aprendan a representar una ecuación del tipo ax+b=cx+d con a,b,c y d enteros positivos en la balanza. Hay varios elementos en esta escena que pueden necesitar explicación o tutoría.

Indicar que la ecuación de la parte superior de la escena es la que hay que representar en la balanza.
Pedir a los alumnos que observen el efecto en las expresiones algebraicas (en la base de la balanza) de la acción de poner una pesa, y que observen que van actualizándose como un efecto de poner bloques. El ejercicio quedará completado cuando las dos expresiones coincidan, cuando aparezca el signo de igualdad.

Balanza 3

En la balanza 3 ya se pide a los alumnos que resuelvan ecuaciones usando el modelo de la balanza. Es la culminación de las dos anteriores. Nótese el contraste con la balanza 2, en la que se pide representar una ecuación con la balanza. Ahora se les pide resolver una ecuación utilizando la balanza.

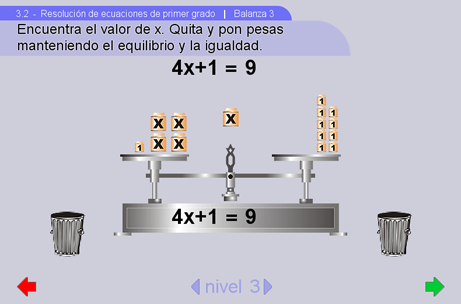
Sugerencias didácticas

Abrir la balanza 3. El programa generará, de forma aleatoria, una ecuación. Y automáticamente representará esa ecuación con bloques en la balanza.
Pedir a los alumnos que observen la ecuación y que en su cuaderno encuentren cuánto pesa el bloque x. Dígales que los únicos datos que tienen es que los bloques que están del lado derecho pesan lo mismo que los que están del lado izquierdo.
Una vez que ya intentaron resolver el problema, puede pedírsele a alguno que pase al pizarrón electrónico a resolverla y que trate de explicar el razonamiento que siguió.
En ese momento hay que remarcarles que si se tira un bloque de un lado, hay que quitar el mismo peso del otro para que la balanza quede equilibrada. Y continuar este proceso hasta que sólo quede un bloque de peso x de un lado y bloques de peso 1 del otro de tal forma que la balanza esté equilibrada.

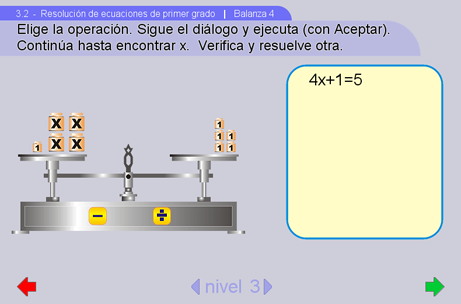
Balanza 4

El objetivo de la balanza 4 es que los alumnos se vayan desprendiendo del modelo de la balanza y se queden sólo con la manipulación algebraica. Nótese que ya no se permite mover los bloques de la balanza. Sólo se puede controlar a la balanza por medio de los botones de "menos" y "entre" (en la base de la balanza). El problema a resolver aquí, de nuevo, es encontrar el valor de x. Pero a diferencia de la balanza 3, la cual enfatiza la manipulación de las pesas, aquí se enfatizan las operaciones algebraicas. Por ejemplo, si se presiona el botón de "-" se preguntará cuántos bloques (y de qué tipo) se desean tirar a la basura de ambos lados de la balanza.

2. Balanza y Poleas

Balanza y poleas 1

La balanza 5 fue diseñada para que los alumnos aprendan a representar una ecuación del tipo ax+b=cx+d con a,b,c y d enteros positivos o negativos en la balanza. El grado de dificultad aumenta debido a la presencia de coeficientes y términos independientes negativos.

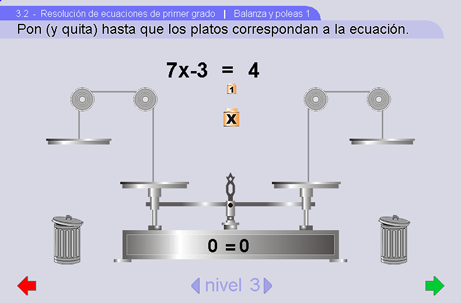
El objetivo es representar una ecuación con la balanza. Las operaciones son quitar y poner pesas en los platos de la balanza. Para poner, se toman de la parte central superior, y para quitar se tiran a la basura. Un objetivo adicional es que se familiaricen con el modelo, antes de entrar a usarlo para resolver ecuaciones.

Sugerencias didácticas

La escena es bastante intuitiva. Sin embargo, a pesar de que se trató de que fuese autocontenida, hay varios elementos en esta escena que pueden necesitar explicación o tutoría:

Indicar que la ecuación en la parte superior de la escena es la que hay que representar en la balanza.
Pedir a los alumnos que observen el efecto en las expresiones algebraicas (en la base de la balanza) de la acción de poner una pesa, y que observen que las expresiones algebraicas van actualizándose como un efecto de poner pesas (bloques) en los platos.
Si no lo descubrieran por sí mismos, puede ser necesario explicarles que poner una pesa en el plato de la polea (plato superior) equivale a restar en la ecuación. Ejemplo: 3x - 6 = 0 se representa con tres pesas del tipo x en el plato inferior izquierdo y 6 pesas unitarias en el plato superior izquierdo.
De manera operativa, se les puede explicar que los platos superiores representan la sustracción; y recordarles que lado izquierdo de la ecuación es el lado izquierdo de la balanza, y lo mismo es cierto de los lados derechos.

Balanza y poleas 2

Ahora se desea que los alumnos resuelvan ecuaciones usando el modelo de la balanza con poleas. En este caso, las pesas ya están colocadas en la balanza y las operaciones válidas son quitar pesas de los platos (tirando a la basura) y poner pesas ya sea tomándolas de arriba al centro, o bien pasando pesas de un plato a otro (transponer).

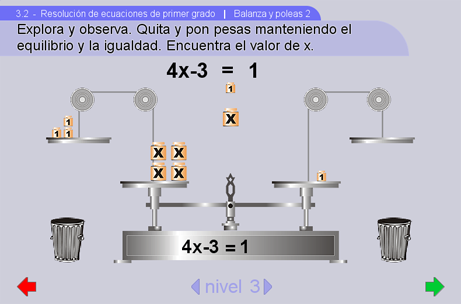
Sugerencias didácticas

Se les debe insistir en que lo que tienen que hacer es quitar y poner pesas de tal manera que se logre dejar sola una pesa x en un lado (por ejemplo el lado izquierdo) y pesas unitarias en el otro, pero al mismo tiempo dejando la balanza equilibrada.

Se espera que, después de explorar un poco, los alumnos lleguen a la idea de transposición de términos de un lado a otro de la balanza (y por lo tanto, de la ecuación). Aquí puede ser necesario ayudarles pidiéndoles que observen que las pesas en el plato superior jalan el plato inferior hacia arriba, pero que eso mismo se puede lograr poniendo las mismas pesas en el plato inferior del otro lado. Quizá el tutor vea la necesidad de pedirles que comprueben eso mediante exploración.

Después de entender lo anterior, deben ser capaces de llegar a poner todas las pesas en los platos inferiores, con pesas x en un lado y pesas unitarias en el otro, y manteniendo el equilibrio de la balanza. (La idea del equilibrio como una metáfora de la igualdad debe ser enfatizada por el tutor durante toda la sesión.)

Para lograr obtener el valor de x se les podría ayudar sugiriéndoles que exploren quitar una x de un lado y ver cuántas pesas unitarias deben quitar del otro para que el equilibrio se mantenga. Si descubren eso ya pueden continuar hasta el final dejando una x en un lado y pesas unitarias en el otro, como se quería.

Ahora bien, es conveniente que el tutor enfatice la operación de división que queda involucrada antes de despejar la x (dejar sola una x de un lado y pesas unitarias del otro). Para que lo descubran se les puede pedir que piensen cuánto debe ser el valor de x si en un plato tienen mx y en el otro un múltiplo de m en pesas unitarias. Se espera que descubran que la división entre m es la operación adecuada. Y si no lo descubren el profesor debe sugerirlo y proporcionarles la ayuda ajustada a sus necesidades cognitivas.

Balanza y poleas 3

Como en Balanza 4 del apartado anterior, este ejercicio está pensado como una transición hacia la operatividad algebraica dejando atrás el modelo de la balanza. Es decir, trata de que los alumnos se independicen del modelo visual de la balanza y apliquen las reglas del álgebra al resolver una ecuación. Es por eso que se les pide explícitamente que ejecuten las operaciones adecuadas para resolver la ecuación, es decir, dejar sola una x en un lado de la balanza y pesas unitarias en el otro (manteniendo la balanza equilibrada).

La pantalla de inicio muestra una balanza ya con pesas en los platos y en un cuadro a la derecha la ecuación que representa. El alumno debe elegir una operación y ejecutarla. Y debe repetir esas dos operaciones (elegir y ejecutar) hasta llegar a encontrar el valor de x.

Primero escogiendo operaciones y luego usando pulsadores, el alumno debe ser capaz de encontrar el valor de x

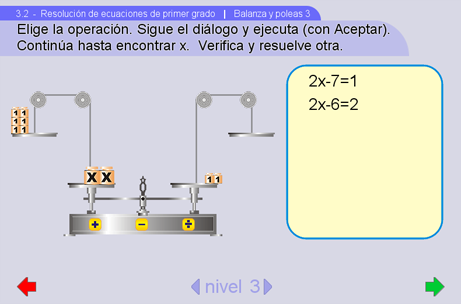
Sugerencias didácticas

Puede ser conveniente que el tutor enfatice de alguna manera que el objetivo es despejar x. Y que la elección de las operaciones debe convertir la ecuación en otra equivalente pero más cercana a x = m.

Se les puede sugerir que un subobjetivo podría ser tener de un lado sólo x y del otro sólo un número. Y también que es mejor no tener signos negativos, etc. (El tutor debe usar su sentido común para proporcionarle la ayuda ajustada al alumno de acuerdo con los resultados que éste vaya obteniendo. Y no debe apresurarse a decirle cómo hacer la tarea. Es mejor dejar que los alumnos exploren las posibilidades y ayudarles un poquito cada vez, hasta que logren el objetivo de despejar x y así resolver la ecuación.

Aunque el estudiante tiene a la vista la balanza y la ecuación, podría ser necesario insistir en la correspondencia entre las dos. Pero también puede ser necesario insistir en que la ecuación tiene prioridad, es decir, que la ecuación es la que hay que ver para poder decidir qué operación ejecutar.

También importa que el tutor haga que sus alumnos observen el efecto en la balanza que son el resultado de ejecutar las operaciones. (Aquí los papeles se invierten: las operaciones tienen un efecto en la balanza y no como en la anterior en que la manipulación de las pesas en la balanza tenía un efecto en la ecuación.)

3. Ejercicios

Este apartado consta de 2 escenas. En ambas se presentarán diversas ecuaciones junto con una herramienta que les ayudará a despejarlas. La diferencia entre las dos escenas es la forma de uso.

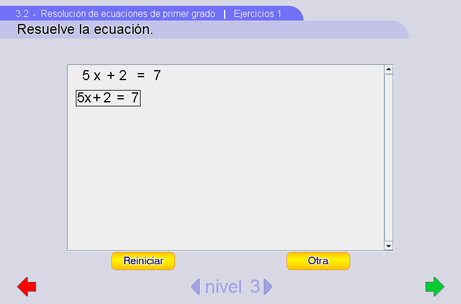
Ejercicios 1

Al iniciar la escena se mostrará una ecuación (generada aleatoriamente) y abajo de esta aparecerá un cuadro de texto con la misma ecuación precargada. El programa permite sustituir la ecuación del cuadro de texto por otra que sea equivalente a la anterior. Cuando se termine de escribir la ecuación en el cuadro de texto hay que presionar la tecla Intro. Si la ecuación introducida mantiene la equivalencia, entonces se aceptará la ecuación y se recorrerá el cuadro de texto un renglón. De esta forma, el estudiante puede ir simplificando la ecuación hasta resolverla.

Para moverse dentro de una expresión (ir al numerador o al denominador de una fracción) basta usar las flechas <- y -> del teclado. Las flechas para arriba y para abajo sirven para pasar del denominador al numerador de una fracción o viceversa, respectivamente. Para escribir una fracción se debe usar el símbolo "/" del teclado. En ese momento aparecerá una plantilla donde se podrá introducir el numerador y denominador.

En la parte inferior hay unos pulsadores para modificar el nivel de dificultad de las ecuaciones. Con el botón Reiniciar se limpiará la pantalla y se permitirá volver a resolver el ejercicio. Al presionar el botón Otra se generará aleatoriamente una ecuación de la misma forma según el nivel.

Ejercicios 2

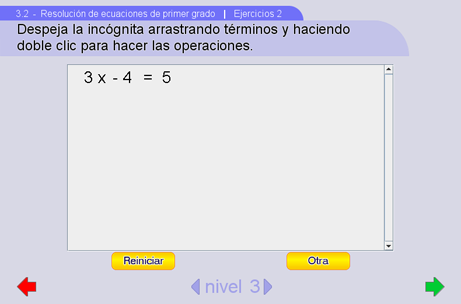
Esta escena es muy parecida a la anterior. La diferencia es que aquí el alumno podrá arrastrar los términos de las ecuaciones de un lado al otro. También podrá efectuar operaciones entre términos con tan sólo hacer doble clic en el símbolo de operación.

Al hacer un doble clic sobre un operador la operación indicada se realiza y aparece la expresión resultante en el siguiente renglón.

4. Problemas

Esta sección consta de dos escenas que ayudan a resolver 2 problemas diferentes. La forma de uso es la misma en las dos.

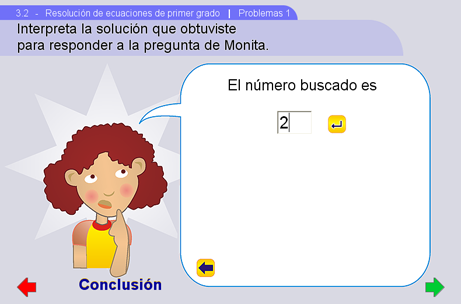
Cada escena tiene 4 partes: Problema, Planteamiento, Resolución y Conclusión. Por medio de las flechas azules en fondo amarillo (ubicadas en la parte inferior del cuadro de diálogo) se puede navegar secuencialmente por cada parte.

La parte Problema simplemente es el enunciado del problema. Una vez que se haya leído el problema, se puede ir a la siguiente parte haciendo clic en la flecha azul.

En la parte de Planteamiento, se le pide al alumno que rellene una tabla para pasar el enunciado del problema a símbolos. Si se hace doble clic en una celda de la tabla, aparecerá un teclado con el que se podrán introducir las respuestas. Se podrá avanzar a la parte Resolución una vez que hayan rellenado correctamente la tabla.

En la parte de Resolución aparece la ecuación ya planteada y el alumno puede despejar la x, arrastrando términos de un lado a otro y haciendo doble clic en los símbolos de operación para poder simplificar.

Por último, la parte de Conclusión pide que se introduzca en un campo de texto la respuesta correcta.