Unidad 3.4

Ángulos interiores de un polígono

RES

Propósito

En esta sesión el estudiante explorará diversos interactivos que lo ayudarán a deducir la fórmula de la suma de los ángulos internos de un polígono. La forma propuesta de encontrar la fórmula es por medio de triangulaciones. En esta unidad se muestran triangulaciones donde los vértices de cada triángulo son vértices del polígono. Es importante aclarar que hay otros tipos de triangulaciones, por ejemplo la que se logra agregando un punto dentro del polígono y trazando segmentos de este punto hacia los vértices.

Instrucciones generales

La unidad se divide en 3 apartados:

Los tres botones que se encuentran en la parte derecha tienen la función siguiente:

Brinda acceso a la ayuda de las escenas interactivas

Herramientas de Enciclomedia

Cerrar la ventana

Uso de campos de texto

En algunas escenas aparecen campos de texto para que el usuario escriba en ellos valores o expresiones numéricas. La forma de uso de estos campos es la siguiente:

1. Cuando se introducen valores en los campos de texto es necesario oprimir al final la tecla Intro. Si al lado del campo de texto hay un botón con el símbolo éste tendrá la misma función que presionar la tecla Intro.

2. El símbolo "^" se utiliza para elevar a una potencia (2^3 = 2³). En caso de escribir una expresión numérica como 2^3+4 (2³+4) al presionar la tecla Intro lo que aparecerá será el resultado de la operación, en este caso 12.

Uso de tablas

Para introducir valores es necesario ir dando clic en cada una de las celdas donde se tiene que colocar el resultado, y para comprobar los resultados introducidos hay que presionar el botón Verificar. Las respuestas correctas aparecerán en color verde y las incorrectas en rojo.

Uso de calculadora

Al hacer doble clic en un campo de texto o en una de las celdas de una tabla aparecerá una calculadora o un teclado virtual.

En ambos casos al terminar de introducir los datos se debe presionar el botón Aceptar; en este momento desaparecerá la calculadora y aparecerá el último resultado escrito en ella.

1. Triangulación

Este apartado consta de 4 escenas.

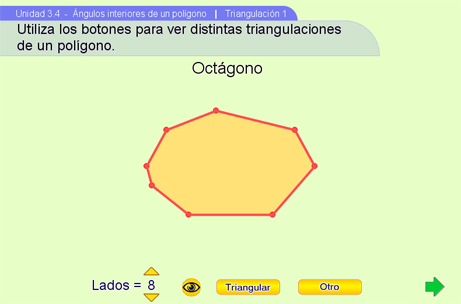
Triangulación 1

El objetivo de esta escena es que el alumno explore las distintas formas de triangular un polígono convexo. Con ayuda de los pulsadores se puede modificar el número de lados del polígono. Al presionar el botón Otro el programa generará (de forma aleatoria) otro polígono convexo con el mismo número de lados que el actual. El botón Triangular mostrará otra triangulación del mismo polígono.

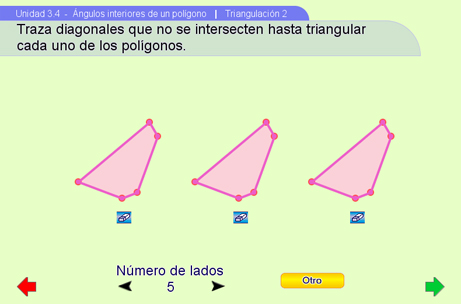
Triangulación 2

Al abrir esta escena aparecerán 3 polígonos idénticos los cuales se pueden manipular a través de los pulsadores (para modificar el número de lados), y del botón Otro (para cambiar la forma). En cada uno de los polígonos se pueden trazar diagonales para lograr una triangulación del polígono. Para trazar una diagonal, primero se tiene que elegir uno de los vértices del polígono y arrastrar el puntero hasta otro de los vértices. Si se intenta trazar una diagonal que se intersecte con otra trazada anteriormente se mostrará un mensaje informativo y no se dibujará tal diagonal. Al presionar el botón se borrarán todas las diagonales trazadas sobre polígono correspondiente.

Es importante que los alumnos tracen tantas triangulaciones como les sea posible y que observen que, dejando fijo el número de lados y cambiando la forma, el número de diagonales necesarias para formar una triangulación se mantiene constante.

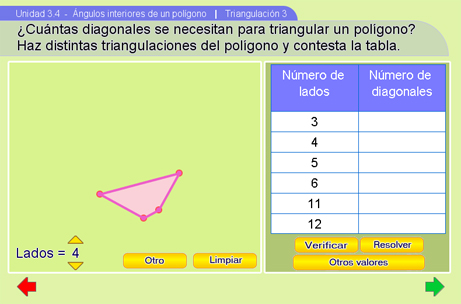
Triangulación 3

Triangulación 3 pide que el alumno llene una tabla con el número de diagonales de un polígono en función del número de lados.

A la izquierda de la tabla aparece un polígono el cuál se puede manipular a través de los pulsadores (para modificar su número de lados), y del botón Otro (para modificar la forma). También se podrán trazar diagonales y limpiar lo dibujado hasta el momento (con el botón Limpiar). Para trazar una diagonal se debe seguir el mismo procedimiento que en la escena anterior. El alumno podrá utilizar esta herramienta para llenar la tabla.

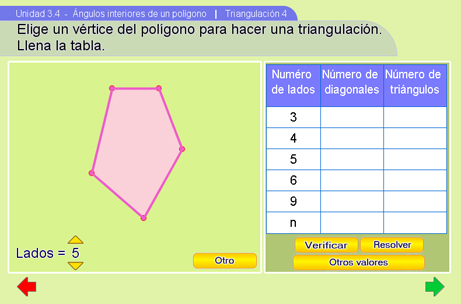
Triangulación 4

Esta escena también pide llenar una tabla: el número de diagonales y el número de triángulos en función del número de lados. Al igual que la escena anterior, se presenta un polígono con el que se podrá explorar para ir llenando la tabla. En esta ocasión se presentarán sólo las triangulaciones donde las diagonales del polígono parten de un mismo vértice. La forma de interacción se explica por si misma en la escena.

Sugerencias didácticas

Las cuatro escenas de este apartado le permiten al alumno experimentar con las triangulaciones de polígonos convexos y lo llevan a conjeturar la fórmula general para calcular el número de triángulos en una triangulación (con diagonales) de un polígono de n lados.

• Pídale a un alumno que explore la escena Triangulación 1. Hágales preguntas y sigan explorando para llegar a una definición intuitiva de qué es una triangulación.
• Avance a Triangulación 2 (presionando la flecha verde). Pida a los estudiantes que dibujen en su cuaderno un polígono igual a los 3 mostrados y que lo triangulen. Elija a uno de sus estudiante y pídale que trace diagonales en cada uno de los polígonos. Haga preguntas como las siguientes: ¿Se podrán construir otras triangulaciones distintas a las que hemos trazado?, ¿cuántas diagonales hay que dibujar para lograr triangular el polígono?, cuando se deja fijo el número de lados y se cambia la forma, ¿qué pasa con el número de diagonales?, etc.
• Avance a la escena Triangulación 3 y pida a los alumnos que llenen la tabla en su cuaderno pues les será de utilidad.
• Elija a algún estudiante para experimentar con la escena. Es posible que los estudiantes decidan empezar a llenar la tabla basándose solamente en observar un caso particular. Si esto sucede invítelos a usar los botones de Otro y Limpiar para que conjeturen que no importa la forma del polígono, si se mantiene fijo el número de lados se tendrá siempre el mismo número de diagonales.
• La escena Triangulación 3 se podría trabajar de manera similar

---

2. Ángulos internos

Este apartado consta de 3 escenas.

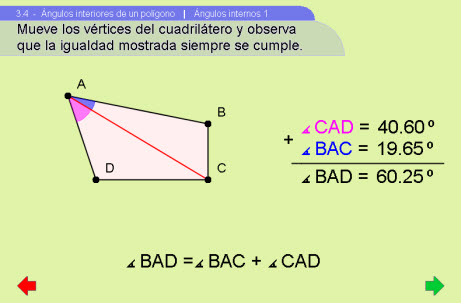
Ángulos internos 1

Es una escena de exploración para enfatizar que la suma de los dos subángulos que se obtienen al trazar una diagonal desde el vértice A es igual al ángulo en A. En esta escena se pueden mover los vértices del cuadrilátero. Observe que la triangulación puede cambiar y con ello la igualdad mostrada.

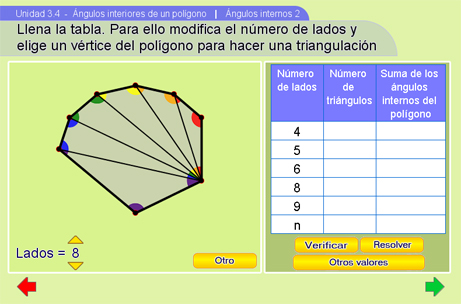
Ángulos internos 2

Esta escena pide llenar la tabla con el número de triángulos y la suma de los ángulos internos de un polígono. De nuevo se podrán hacer triangulaciones del polígono (que aparece a la izquierda de la tabla) con tan sólo elegir uno de sus vértices y esta vez se mostrará una ayuda visual desplegando los ángulos internos de cada triángulo con un color distinto para cada triángulo. Es momento de recordarle a los alumnos que la suma de los ángulos internos de un triángulo es 180 grados. Sabiendo esto, y con la ayuda de ángulos coloreados, se espera que los alumnos lleguen a la expresión (n-2)*180 que calcula la suma de los ángulos internos de un polígono de n lados.

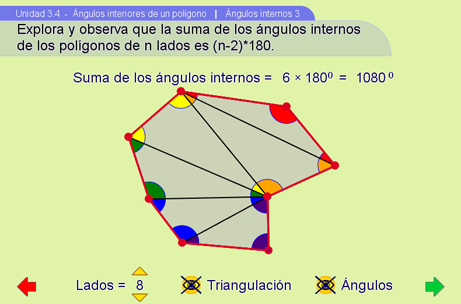
Ángulos internos 3

Esta escena es de exploración. Se presentará un polígono regular que se podrá modificar moviendo los vértices para formar cualquier polígono incluyendo los no convexos. Con los pulsadores se podrá modificar el número de lados. Hay botones para mostrar u ocultar la triangulación y los ángulos determinados por ésta

3. Problemas

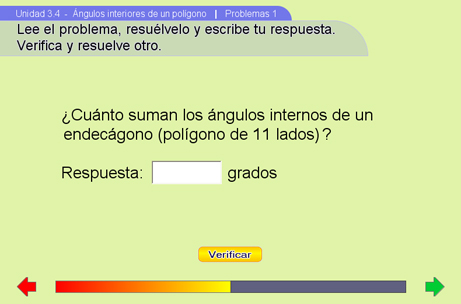
Problemas 1

En esta escena se propondrán ejercicios del tipo ¿Cuánto suman los ángulos internos de un n-ágono? (con n un número no tan grande y mayor que 3)
Estos ejercicios se resolverán fácilmente aplicando la fórmula que se obtuvo en Ángulos internos 2 y 3. Se podrá introducir la respuesta mediante un campo de texto y presionando el botón verificar. En este momento se presentará otro ejercicio del mismo tipo o bien se dará la oportunidad de contestar de nuevo si se responde de forma errónea.

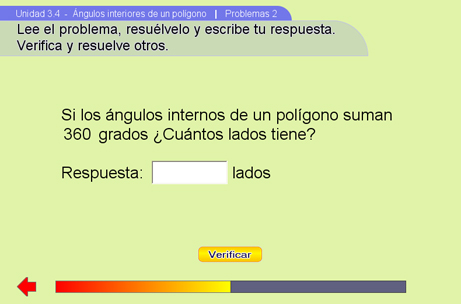
Problemas 2

Se propondrán ejercicios del tipo Si los ángulos internos de un polígono suman X, ¿cuántos lados tiene dicho polígono?
Se podrá introducir la respuesta mediante un campo de texto y presionando el botón verificar.

---

Créditos

Autora
Valentina Muñoz Porras

Colaboraciones
José Luis Abreu León propuso la escena Triangulación 2, creó la idea de la escena Ángulos internos 3 y desarrolló la primera versión.

Agradecimientos
A la Dra. Teresa Rojano Ceballos por su invaluable asesoría en diseño didáctico, en el seminario de los martes en el ILCE. Su sabiduría y estilo comunicativo saben convencer y hacer que emerja un producto didáctico grupal.

---

Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes.
Como la unidad utiliza el applet Descartes, propiedad del Ministerio de Educación de España,
sus contenidos se distribuyen bajo una licencia de Creative Commons.