Unidad 3.5
Cubrimientos del plano
RES
Propósito
Que el alumno conozca las características de los polígonos que permiten cubrir el plano y que realice recubrimientos de éste desarrollando su percepción del plano y sus habilidades para manipular figuras geométricas simples y complejas.
Instrucciones Generales
Esta unidad contiene 5 apartados:
- Inicio
- Polígonos
- Tramas
- Patrones
- Mosaicos
- Creación
artística

Los tres botones que se encuentran en la parte derecha tienen
la función siguiente:

Brinda acceso a la ayuda de las escenas interactivas
 Herramientas Enciclomedia
Herramientas Enciclomedia
 Cerrar
Cerrar
0. Inicio
La sección Inicio
permite entender
algunas herramientas de esta unidad, así mismo es la que aparece
al iniciar el programa.
1. Polígonos
Instrucciones
En esta actividad cada figura puede moverse de lugar tocando su centro y arrastrándolo hasta la posición deseada, también pueden girarse apoyándose en el aro que hay alrededor del centro seleccionado, el manejo del control es muy fácil una vez comprendido.
Para ver una explicación de cómo utilizar el control de rondana para mover y girar las figuras vea el apartado Inicio.
Con el botón Mostrar centros aparecen como guía puntos centrales en cada figura.
Sugerencias didácticas
El profesor, en esta actividad, puede pedir a los alumnos que le describan los movimientos que tiene que hacer él para cubrir el plano. Con los triángulos y cuadrados es rápido de hacer, conforme se avanza el proceso se va complicando.
Es importante fijarse que orden guardan los centros de las figuras, eso dará una idea de las propiedades que tiene cada cubrimiento en particular; por ejemplo, los centros de los triángulos parecen ser los vértices de hexágonos y los centros de los cuadrados parecen ser los vértices de otros cuadrados. Para ver este detalle puede, una vez armado el mosaico pueden unirse los centros con los plumones del pizarrón electrónico.
Es interesante discutir con los alumnos que sucede en las demás figuras. De forma opcional, para facilitar la comprensión de este hecho, puede hacerse una tabla donde se llene horizontalmente el número de figuras que concurren en un vértice y el número de figuras pegadas a otra figura; verticalmente se colocan las figuras que aparecen en las diferentes escenas a excepción del pentágono irregular (éste tiene varios tipos de vértices). Una vez llenada la tabla, se puede ver que los números del triángulo y del hexágono son los mismos pero al revés. Discútase en clase que tiene que ver esto con el orden de los centros.
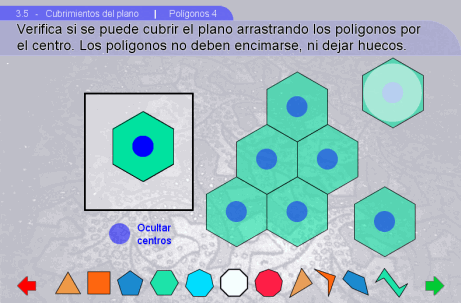
2. Tramas
Instrucciones
El menú desplegable permite
escoger el recubrimiento que uno quiera seleccionando un tipo de
figura. Cabe mencionar que algunas figuras pueden cubrir el plano de
diferentes formas.
Puede arrastrarse el recubrimiento en todas las direcciones para
apreciarlo mejor.
Sugerencias didácticas
El profesor, en esta actividad,
puede comenzar preguntando si hay varias formas de llenar el plano con
triángulos. Para mostrar a los alumnos que a veces si hay varias
formas, se puede selecciona del menú las figuras que tienen 2
opciones. En el caso de los triángulos, puede dejarse la tarea
de encontrar otra forma distinta (de las aquí expuestas) de recubrimiento del plano.
En el caso de los pentágonos y de los heptágonos se puede observar que, al momento de intentar llenar el plano, quedan agujeros de diversas formas entre las figuras. En estos ejemplos, los agujeros están pintados de diferentes colores. (En estos ejemplos, los agujeros son todas las figuras que no son ni pentágonos ni heptágonos regulares).
Un dato interesante es que, a la
fecha no hay un estudio completo de este tipo de agujeros, y
prácticamente cualquier pregunta que se ocurra sobre ellos no se
ha estudiado.

3. Patrones
Este apartado nos muestra como cubrir el plano con triángulos, cuadriláteros y hexágonos.
Instrucciones
La figura base para cubrir el plano tiene círculos de color rojo que pueden moverse libremente para crear diferentes triángulos, cuadriláteros y hexágonos.
Sugerencias didácticas
Aquí es conveniente el tratar de imitar las figuras irregulares de la actividad anterior a partir de las figuras regulares que aparecen en cada escena moviendo los círculos rojos de los vértices.
El caso del pentágono regular es de gran importancia, ya que es la única figura presentada aquí con la que no se puede cubrir el plano.
Puede invitar a los alumnos a tratar de explicar alguna razón por la cual no se pueda.
Una respuesta podría ser que se fijen en los vértices de las figuras en los cubrimientos anteriores. En ellos, la suma de los ángulos que se forman es de 360° (Por ejemplo en el cuadrado, son 4 ángulos de 90° por cada vértice, 4x90°=360°). Los pentágonos tienen ángulos de 144°, si sumo dos de estos ángulos obtengo 288°, y si sumo tres obtengo 432°. Con dos no alcanzo 360° y con tres me excedo. Así se puede ver que es imposible formar un ángulo de 360° de forma correcta. Puede explicarse esto fácilmente utilizando el apartado "Polígonos".
Otra buena actividad es que traten
de dar reglas para pegar las figuras a partir de lo observado
utilizando el siguiente cuento.
Al no saber como, los trabajadores llamaron al artista al lugar donde trabajaba para pedirle instrucciones precisas por teléfono. ¿Puedes dar las instrucciones que seguramente dio el artista?
A lo que tienen que llegar los alumnos es que, para llenar el plano con triángulos, es suficiente con pegarlos por sus lados iguales. Para los cuadriláteros se puede observar que se colocan haciendo líneas rectas con sus diagonales (rectas que unen vértices opuestos).
Por último, con los hexágonos no siempre se puede cubrir el plano. Para que sea posible es necesario que tengan sus lados opuestos paralelos, como los mostrados aquí. Las reglas para pegarlos son muy similares a las de los cuadriláteros, solo hay que escoger dos diagonales que no sean paralelas y seguir los mismos pasos.
Hay otras maneras de dar instrucciones, aquí solo mostramos una por cada figura.

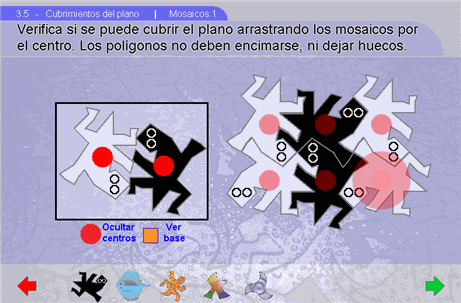
4. Mosaicos
Este apartado nos
enseña diferentes mosaicos y nos reta a descubrir como llenar el
plano con ellos.
Instrucciones
El manejo del control es igual que
el del apartado
"Polígonos". Para
ver una explicación de como utilizar el control de rondana, para
mover y girar las mosaicos, vea el apartado Inicio.
Con el botón Mostrar centros aparecen como guía puntos centrales en cada mosaico artístico.
Con el botón Mostrar figura base aparece encima de cada mosaico artístico la figura que se recortó para obtener la pieza. Este detalle se expone en el apartado Creación artística.
Sugerencias didácticas
También es útil el fijarse bien de donde se cortan las partes de la lagartija que se pegarán en un lado determinado. Lo mismo hay que hacer con las demás figuras.
5. Creación
artística
Instrucciones
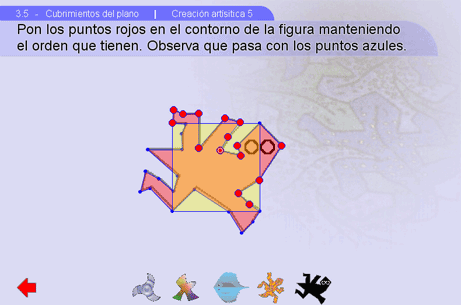
Prácticamente sólo hay que observar. Puede escogerse la figura que uno quiera apreciar en el submenú inferior.
Al seleccionar la lagartija negra y blanca se accede a una escena donde se pueden hacer figuras que cubren el plano. Para apreciarlo, se pueden arrastrar los puntos rojos sobre el contorno de la lagartija.
Sugerencias didácticas
Esta
actividad nos ayuda a entender como podemos fabricar nuestros propios
mosaicos artísticos, aunque no es algo fácil.
Puede organizarse un concurso, pedirle a los chicos que creen figuras
de la misma manera que se observa en esta actividad. Puede darse un
premio a la figura más original que se les ocurra en el
salón. Para mayor información véase
bibliografía referente a M. C. Escher.
Datos curiosos sobre los mosaicos:
- Son de gran
utilidad al estudiar las estructuras microscópicas de los
cristales, como los cuarzos, los diamantes, los zafiros, la sal, el
hielo, los rubíes, etc.
ya que su estructura cristalina asemeja mosaicos.
- En la industria se utilizan
para crear bellos dibujos para
textiles, material de
construcción (mosaicos y losetas), tapices, etc, ya que, por
repetir el mismo patrón,
se producen de forma sencilla
y barata.
- En la creación de aleaciones es de suma importancia, ya que, el orden en el que se acomodan las moléculas da diferentes propiedades físicas a los materiales.
- Los árabes conocían todos los grupos de simetrías para formar mosaicos periódicos mucho antes de que se comenzaran a estudiar en occidente ya hace varios siglos. Pueden verse actualmente casi todos los posibles grupos en "La Alambra" ubicada en España.
Créditos
Autor
Claudio Francisco Nebbia Rubio
Agradecimientos
A Oscar Escamilla González
y
José Luis Abreu León, integrantes del Grupo
Descartes, por colaborar ampliamente con valiosas ideas en la
realización de esta
unidad.
Reconocimientos
El apartado "Creación
artística" se inspira y utiliza ideas
que
Enrique
Martínez Arcos plasma
en las escena "MOSAICOS DE ESCHER" ubicadas en
http://descartes.cnice.mec.es/materiales_didacticos/escher/escher.htm
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes.
Como la unidad utiliza el applet Descartes, propiedad del Ministerio de Educación de España,
sus contenidos se distribuyen bajo una licencia de
