Unidad 5.1

Sistemas de ecuaciones

RES

Propósito

Que alumno pueda plantear, resolver, concluir y comprobar por si mismo los problemas propuestos. Que comprenda la importancia de estos ejercicios para pasar de un problema cotidiano a un ejercicio matemático.

Instrucciones generales

La unidad se divide en cuatro apartados:

1. La solución es
2. Problemas
3. Métodos
4. Ejercicios

Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.

Los tres botones que se encuentran en la parte derecha tienen la función siguiente:

botones 1 Brinda acceso a la ayuda de las escenas interactivas

botones 2 Herramientas de Enciclomedia

botones 3 Cerrar la ventana

1. La solución es

Este apartado consta de una sola escena, con la que pretendemos introducir al alumno a la resolución de sistemas de dos ecuaciones con dos incógnitas a través de la gráfica de puntos en el plano cartesiano, los cuales satisfacen los enunciados planteados.

Esta escena consta de tres etapas, en la primera se propone un problema y se le pide al alumno localice tres puntos que cumplan con la primera condición que se pide. Cada que coloque un punto debe dar clic al botón Fijar punto.

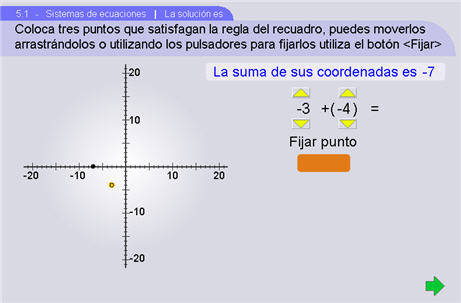
Si el ejercicio lo hizo bien, al momento de verificar, se graficará la recta. De esta forma, pasamos a la segunda etapa de esta escena, en donde se pide graficar otros tres puntos que satisfagan la segunda condición, lo cual dará lugar a otra recta en el plano cartesiano.

Si lo hizo mal, tiene que mover el o los puntos a la posición adecuada con ayuda de sus coordenadas que aparecen del lado derecho y después dar clic al botón Verifica. Una vez hecho esto, pasamos a la segunda etapa.

Cuando se equivocan en dos o tres puntos:

Cuando se equivocan en un solo punto:

Ya que están graficadas ambas rectas, se señala el punto de intersección. Para poder mover el punto rojo por una u otra recta se le dan clic a los botones R1 o R2, el primero para la recta verde y el segundo para la azul. Al ir moviendo el punto por las rectas se observan sus coordenadas, tanto en el plano cartesiano como sustituidos en las ecuaciones correspondientes, donde se comprueba la solución.

Sugerencias didácticas

Debido a que es una escena introductoria, no se deben plantear las ecuaciones para resolver el sistema de ecuaciones. La aparición de estas ecuaciones, después de obtener la gráfica de las dos rectas, es sólo para observar y comprobar que el punto de intersección satisface a ambas rectas.

Al momento de realizar la gráfica de cada una de las rectas en el plano cartesiano, se debe dejar muy claro que la existencia de una recta está determinada únicamente por dos puntos. El hecho de encontrar un tercer punto en la recta tiene la finalidad de mostrar que existen muchas otras coordenadas que pueden satisfacer las condiciones, lo que también se refuerza en la última parte.

Después de realizar el ejercicio, se debe enfatizar que el único punto que satisface las dos condiciones es justamente aquél que se encuentra en ambas rectas. Para ello se puede hacer uso de la sustitución que se va llevando a cabo al momento de ir moviendo el punto rojo en las rectas R1 y R2. Y ese punto, en la intersección es la solución del sistema de dos ecuaciones con dos incógnitas.

2. Problemas

En las escenas de este apartado, el alumno aprenderá cómo se plantea, resuelve, concluye y comprueba un sistema de ecuaciones. La funcionalidad de todas ellas es exactamente la misma, lo que va a cambiar es el nivel de dificultad, por lo que daremos las instrucciones sólo para las escenas uno y tres.

Como mencionamos, la complejidad de las escenas va a ir variando conforme se vaya avanzando, podemos dividirlas en tres bloques. El bloque 1 consta de las primeras dos escenas (Problemas 1 y 2) en donde conocemos el valor de una de sus incógnitas (x=a, y=b). En las ecuaciones del bloque 2 (Problemas 3 y 4), una de sus incógnitas está en términos de la otra (x=ay, y=bx). La última escena (Problemas 5) pertenece al bloque 3, en donde una de sus dos ecuaciones es de la forma x=y+a o y=x+b.

Para la resolución de ecuaciones hicimos uso del método de sustitución, ya que es la forma más natural de realizarlo debido a la presentación de las ecuaciones.

Problemas 1

En esta escena el alumno deberá leer con mucha atención las indicaciones, ya que en ellas están especificados los datos con los que debe plantear las ecuaciones oprimiendo los pulsadores. Para comprobar estos planteamientos y avanzar a la siguiente escena el estudiante pulsará el botón Resolución.

Ahora el alumno observará cómo se resuelve el problema paso a paso, pulsando los botones que van apareciendo hasta ver la solución del problema.

El estudiante podrá observar cómo se resuelve el sistema de ecuaciones y cuáles son las conclusiones de este resultado. Si oprime el botón Planteamiento regresará a la primera escena. Si pulsa el botón Comprobación avanza a la siguiente escena.

Aquí el alumno podrá ver que el resultado de la variable "y" es correcto. Si pulsa el botón "Resolución" regresará a la escena donde se resuelve el sistema. Si oprime el botón "Otro ejercicio" nos dará otros valores con las mismas incógnitas.

Problemas 2

Esta escena, al igual que la anterior, pertenece al primer bloque del conjunto de problemas de este apartado, solo que en este caso se da el valor de la variable y. Por lo que no será necesario dar una explicación detallada de su procedimiento.

Problemas 3

En las siguientes dos escenas (Problemas 3 y 4) el estudiante observará cómo se resuelve un sistema de dos ecuaciones con dos incógnitas por medio del método de sustitución; este sistema tiene la particularidad de que en una de sus ecuaciones la variable x está despejada con respecto a la otra.

El alumno planteará la ecuación a partir de los datos de la nota de remisión debiendo poner especial atención en las especificaciones de las variables, fijándose especialmente en el enunciado que aparece al final de la nota. Finalmente el estudiante pulsará el botón Resolución para verificar sus resultados y pasar a la siguiente escena.

De forma análoga al ejercicio anterior, el alumno observará cómo se resuelve el sistema de ecuaciones paso a paso, conforme se vayan presentando los botones e instrucciones correspondientes hasta llegar a la solución y conclusiones.

Aquí el alumno podrá ver que los valores obtenidos de "x" y "y" son correctos, sustituyéndolos en ambas ecuaciones.

Problemas 4

Esta escena tiene la variable "y" despejada en términos de "x". La funcionalidad de esta escena es la misma que la anterior, ambas pertenecen al bloque 2.

Problemas 5

En este caso, una de las ecuaciones del sistema tiene la variable "y"despejada en términos de "x", de la forma "y=x+a".

Sugerencias didácticas.

Sugerimos que el profesor enfatice la lectura correcta de cada problema planteado para que el alumno pueda comprender claramente su significado. La parte de resolución debe ser obtenida por los propios alumnos en su cuaderno para que entiendan mejor los pasos que deben seguir y después compararla con lo que muestra el interactivo. Las conclusiones y la comprobación se deben hacer en forma grupal, después de que cada alumno la realizó sólo o con un grupo de compañeros para clarificar todo el proceso.

Es recomendable comentar a los alumnos que el método de sustitución no es el único por el cuál se pueden resolver estas ecuaciones, que existen otros igualmente sencillos pero que al final ellos elegirán el más apropiado o el que a ellos se les facilite más.

3. Métodos

Este apartado consta de cuatro escenas, en las cuáles se explicará detalladamente la resolución de sus ecuaciones por medio de los métodos de Suma o Resta y de Igualación.

Métodos 1

En esta escena se plantea un ejercicio que puede resolverse con el método de Suma o Resta. En primer lugar, se debe escribir en la tabla, el sistema de ecuaciones que satisfaga el enunciado planteado: arriba la ecuación para el triángulo y abajo para el rectángulo. Obsérvense las figuritas del lado izquierdo de la tabla. Para ver si las ecuaciones que escribimos son correctas se debe dar clic al botón Verificar e inmediatamente después dar clic al botón Continuar.

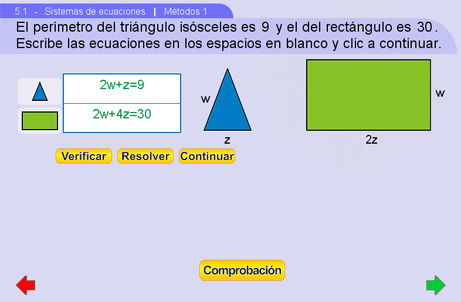
Una vez que tenemos el sistema de ecuaciones, proseguimos a su resolución. Para ello, tenemos cuatro opciones presentadas en un menú, las cuales nos darán una forma diferente de resolver las dos ecuaciones con dos incógnitas con el método de Suma o Resta. Después de elegirlo le damos clic al botón Resuelve.

Cuando le damos clic al botón Resuelve, aparece un recuadro donde se va a poder obtener la solución de la ecuación con una incógnita observada anteriormente. La ecuación se puede resolver arrastrando los números y/o literales al otro lado de la igualdad, o dando doble clic en los signos de igual y/o de las operaciones indicadas. Ya teniendo ese resultado, se debe sustituir en alguna de las dos ecuaciones, para hacerlo se debe dar clic a los botones de Sustitución, azul y verde. Cada uno de ellos debe abrir un recuadro en donde se podrá resolver la ecuación correspondiente. No es necesario sustituir el valor obtenido en las dos ecuaciones si ya se obtuvo en la primera, pero nos puede servir para darnos cuenta que la solución será la misma si lo hacemos en una o en otra ecuación.

Ya que obtuvimos la solución del sistema de ecuaciones, entonces vamos a comprobar si los valores son correctos, para ellos debemos dar clic al botón Comprobación y resolver las ecuaciones sin incógnitas presentadas en los recuadros correspondientes. Obsérvese además los valores sustituídos en las imágenes del triángulo y el rectángulo.

Métodos 2

En la ecuación presentada no es tan intuitivo el uso del método de Suma o Resta. De hecho, se plantea de esta forma para cuestionar al alumno si este es el método más apropiado. Le mostraremos que sí, multiplicando las ecuaciones por un mismo número, que nos ayude a cancelar cualquiera de las dos variables.

Métodos 3

En esta escena utilizamos el método de Igualación, ya que en este caso, de la primera ecuación se puede despejar fácilmente la variable "x" y en la segunda ya está hecho.

Métodos 4

Así como en la escena anterior, una de las ecuaciones ya está despejada y la otra puede despejarse rápidamente, por lo que el uso de este método es muy intuitivo.

Sugerencias didácticas

Como observamos en las cuatro escenas, los ejercicios están planteados de tal forma que el sistema de ecuaciones sea el adecuado para cada método, no obstante el uso de algún otro es correcto. La idea de este apartado es que el alumno tenga las herramientas algebraicas necesarias para resolver cualquier problema que se le presente, ya sea por uno u otro método o también puede obtener sus soluciones de forma intuitiva. Pero es muy importante cuestionarle al alumno porque se utiliza cierto método y no otro en los distintos ejercicios.

4. Ejercicios

Este apartado consta de dos escenas, aquí se puede elegir entre el Métdo de Suma o resta y el de Igualación. Sin embargo, cada ejercicio puede resolverse intuitivamente por un método en particular.

Ejercicios 1

Lo primero que debe hacer el alumno es plantear el sistema de ecuaciones y elegir el método que crea es el más adecuado dando clic a los botones.

Si la elección fue Suma o resta, la escena aparece sólo con un botón del lado derecho llamado Pasa a la forma ax+by=c. Esto ocurre ya que las ecuaciones planteadas están despejadas, la primera para y, la segunda para x.

En este caso, tenemos únicamente dos rutas, Multiplicar la ecuación 2 por 2 o la ecuación 2 por 3, ambas son independientes y las empezamos a resolver dando clic sobre cualquiera de los dos botones.

Elegimos Multiplicar la ecuación 2 por 3, la cuál nos presenta el sistema de ecuaciones reducido a una sola ecuación con una incógnita, la cuál mandaremos al recuadro inferior por medio del botón Resuelve.

Ya obtenido el valor de la x, entonces lo sustituimos en una o en otra de las dos ecuaciones para conocer ahora el valor de y.

Finalmente, comprobamos los resultados. El botón Regresar nos lleva a la primera etapa de la escena, donde elegimos el método por el cuál queremos resolver el sistema de ecuaciones con dos incógnitas.

Al elegir la opción de Igualación, tenemos una escena en donde podemos elegir dos caminos independientes para resolver el sistema utilizando este método. La primera es dando clic a los botones verde y azul con etiqueta Despejar x, la segunda los botones verde y azul llamados Despejar y.

Elegimos los botones para despejar las x´s de las dos ecuaciones e inmediatamente nos aparece un nuevo botón que nos dice que debemos igualarlas.

Después de igualar las ecuaciones, obtenemos una sola ecuación con una incógnita, en este caso y, obteniendo su valor dando clic al botón Resuelve, que va a abrir el recuadro donde se pueden manipular los números y variables de dos formas: arrastrándolos y dando doble clic sobre ellos. De tal forma que obtendremos el valor de y.

Sabiendo el valor de y, lo sustituimos e la ecuación 2, utilizando su botón correspondiente.

Para terminar, comprobamos las soluciones en ambas ecuaciones.

En la siguiente escena Ejercicios 2 se plantea otro ejercicio, el cual se resuelve por medio de los métodos Suma o Resta e Igualación. La funcionalidad es idéntica a Ejercicios 1.

Sugerencias Didácticas

Lo más importante en este apartado no es resolver paso a paso los sistemas de ecuaciones, sino ayudarle al alumno a elegir el método más adecuado. Seguramente muchos de ellos harán su elección de acuerdo a la facilidad que ellos obtengan en uno u otro método, eso no es incorrecto, pero deben conocer las ventajas y desventajas de utilizar uno u otro método. Los alumnos deben resolver esos ejercicios en su cuaderno, ya que en los apartados anteriores se les enseñó paso a paso cada uno de los métodos. Se pueden observar ciertas características, como el tiempo que lleva resolver un sistema por uno u otro método o la facilidad para utilizar uno de ellos, constatando que la solución siempre va a ser la misma.

Créditos

Autora
Alexandra Guzmán Velázquez

Agradecimientos
A María Teresa Rojano Ceballos por sus sugerencias didácticas.

Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes.
Como la unidad utiliza el applet Descartes, propiedad del Ministerio de Educación de España,
sus contenidos se distribuyen bajo una licencia de Creative Commons.