Resumen

1  Descripción del Problema

Supóngase que se tienen cuatro hormigas colocadas en los vértices de un cuadrado de lado l centrado en el origen de nuestro sistema de referencia y con los vértices sobre los ejes. Llámese A al vértice que se encuentra sobre la parte positiva del eje de la x y procédase a etiquetar los vértices en el sentido contrario a las manecillas del reloj B, C, y D. Supóngase ahora que la hormiga en A está enamorada de la que está en B, que la de B está enamorada de la de C, que la de C está enamorada de la de D y ésta lo está de la de A. Cada hormiga camina hacia aquella de la que está enamorada y todas caminan con la misma rapidez. Se pretende conocer la trayectoria que sigue cada hormiga. A partir de este momento se denotará con a a la hormiga cuyo punto de partida es A, con b a la que estaba en B y así sucesivamente.

2  Solución

Sea (x,y) el punto donde se encuentra, al instante t, la hormiga a. En ese momento, dado que todas las hormigas caminan con la misma rapidez, b estará en el punto de coordenadas (-y,x). Es decir en el punto que se obtiene de rotar 90^o=p/2 el punto (x,y). La hormiga a en ese momento estará dirigiéndose hacia (-y,x) que es donde se encuentra b, es decir su vector velocidad tendrá la dirección de la recta con pendiente:

m =  x-y -y-x =  y-x y+x

Considérese esta pendiente como la derivada dy/dx.

Hágase ahora un cambio a coordenadas polares:

x=r cos(q)

y=r sin(q)

entonces:

dy dx =  r sin(q)-r cos(q) rsin(q)+r cos(q) =   sin(q)- cos(q) sin(q)+ cos(q)

Por otra parte:

dx = cos(q)dr -r sin(q) dq

dy = sin(q)dr +r cos(q) dq

De donde:

sin(q)- cos(q) sin(q)+ cos(q) =  sin(q)dr +r cos(q) dq cos(q)dr -rsin(q) dq

Manipulando esta expresión:

(sin(q) - cos(q)) (cos(q) dr - r sin(q) dq) = (sin(q) + cos(q)) (sin(q) dr + r cos(q) dq) Þ

sin(q) cos(q) dr - r sin2 (q) dq- cos2 (q) dr + r sin(q) cos(q) dq =

sin2 (q) dr + r sin(q) cos(q) dq+ sin(q) cos (q) dr + r cos2 (q) dqÞ

(- cos2 (q) - sin2 (q))dr = (r cos2 (q) + r sin2(q) ) dqÞ

-dr = r dqÞ - æ è  1 r ö ø dr = dq

De donde finalmente:

- ln|r| = q+ C

Es decir:

r = e(- q+ C) = K e- q

Dado que el cuadrado está centrado en el origen con los vértices sobre los ejes, cuando q = 0 tenemos que r = l/ Ö2, de donde: K = l/Ö2 y entonces:

r = æ è  l Ö2 ö ø e -q

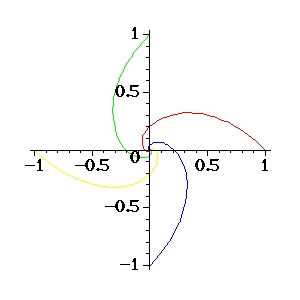
Y ésta es la ecuación que describe una espiral logarítmica, muy conocida por su estrecha relación con la razón áurea y que aparece inesperadamente en la naturaleza. En la figura 1 se puede observar la trayectoria seguida por cada hormiga.

3  Generalización

Es posible generalizar el resultado suponiendo que tenemos a las hormigas acomodadas en los vértices de un polígono regular de n lados centrado en el origen. Cuando una hormiga, a la que se llamará a, está en el punto de coordenadas (r cos(q), r sin(q)) la hormiga a la que persigue, es decir b, está en (rcos(q+ 2p/n), r sin(q+ 2p/n)). Así que la pendiente de la tangente a la trayectoria en ese punto es:

m =  sin(q+ 2p/n)- sin(q) cos(q+ 2p/n) -cos(q)

Recuérdense las expresiones para calcular el seno y el coseno de U+V en términos de los senos y los cosenos de U y V, utilizándolas obtenemos:

m=  sin(q) cos(2p/n) + cos(q) sin(2p/n) - sin(q) cos(q) cos(2p/n) - sin(q) sin(2p/n) -cos(q) =

sin(q) (cos(2p/n) -1) + cos(q) sin(2p/n) cos(q) (cos(2p/n) -1) - sin(q) sin(2p/n) =

sin(q)dr + r cos(q)dq cos(q)dr - rsin(q)dq

De donde:

sin æ è  2p n ö ø dr = r æ è cos æ è  2p n ö ø - 1 ö ø dqÞ

æ è  1 r ö ø dr = æ ç ç ç ç è cos æ è  2p n ö ø - 1 sin æ è  2p n ö ø ö ÷ ÷ ÷ ÷ ø dq

Integrando:

ln|r| = æ ç ç ç ç è cos æ è  2p n ö ø - 1 sin æ è  2p n ö ø ö ÷ ÷ ÷ ÷ ø q+ C

es decir:

r = K e(( cos([(2p)/n] ) - 1)/(sin([(2p)/n] ))) q

Donde K R depende del polígono donde estén colocadas las hormigas y que se espera será de un número par de vértices, de modo que no tengamos que pensar en que las hormigas tengan algún tipo de preferencia sexual no convencional.

4  Longitud de la Trayectoria

En el caso del cuadrado:

r¢(q) = æ è  l Ö2 ö ø e-q (-cosq-sinq, cosq- sinq)

De donde:

|| r¢(q) || = æ è  l Ö2 ö ø e-q Ö2 = le-q