Cálculo del Área de Las Lúnulas

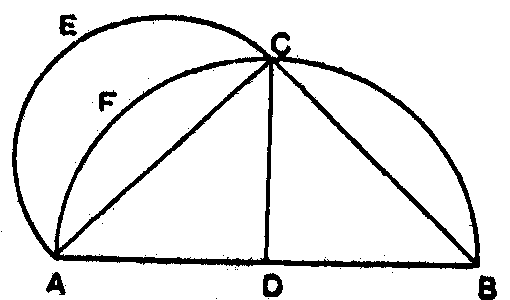
Si sobre los lados de un triángulo recto ACB se describen semicírculos en el mismo lado, la suma de las áreas de las dos lunas AEC, BDC es igual a la del triángulo ACB. Si el triángulo recto es isósceles, las dos lunas son iguales, y cada una de ellas es la mitad del área del triángulo. Así se encuentra el área de una lúnula.

Explícitamente, en la figura abajo, supóngase que AB es el diámetro de un círculo; D, su centro y AC y CB los lados de un cuadrado inscrito en él. Tomando AC como diámetro, describa el semicírculo AEC. Una con CD. Ahora, puesto que AB² = 2AC² y los círculos (y por consiguiente los semicírculos) son uno a otro como los cuadrados de sus diámetros: El semicírculo ACB = 2semicírculo AEC. Pero el semicírculo ACB = 2cuadrante ADC; por consiguiente, el semicírculo AEC = cuadrante ADC. Restando ahora la parte común, el segmento AFC, se tiene: área de la luna AECF = área triángulo ADC. Por tanto, la luna 'se cuadra'.