Construcción del incentro de un triángulo

Construcción

• Construye un triángulo llamando A, B, C a los vértices y a, b y c a los lados opuestos a ellos respectivamente o utiliza uno que hayas construido anteriormente.
• Construye un punto auxiliar D en el interior del triángulo. Para ello, una vez que le das nombre, en el renglón en el que estás trabajando haz click en , automáticamente te llevará a la pantalla gráfica, ahí haz click en cualquier punto interior del triángulo.
• Haz click en , al elegir bisectriz en el menú, aparece un submenú, selecciona En la misma región que un punto. En la casilla escribe l, haz doble clic en el punto b, doble click en c y doble click en D, así hemos dibujado la bisectriz del ángulo A. Repite el procedimiento llamando m a la bisectriz del ángulo B, es decir, entre las rectas a, c y del mismo lado que D. Por último, llama n a la bisectriz del ángulo C (entre las rectas a, b y del mismo lado que D).
• Haz click en y elige en el menú Intersección de rectas. Escribe I en la ventana y haz doble click en dos de las rectas l, m, n.

  
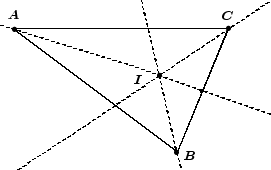
  El punto I es el incentro del triángulo.

  
  En la ventana gráfica selecciona cualquiera de los vértices y muévelo observando qué sucede con el incentro.