1 Leyes
de Kepler
- Primera ley:
La órbita de un planeta alrededor del Sol es una elipse con el sol en
uno de sus focos.
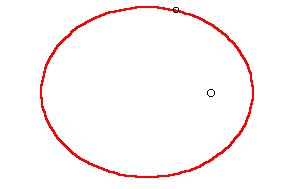
- Segunda ley:
La línea que une al planeta con el Sol barre áreas iguales en tiempos
iguales.
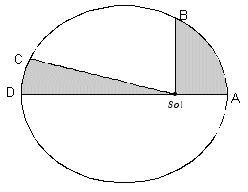
- Tercera ley:
El cuadrado del período de un planeta es proporcional al cubo de su semieje
mayor.
La demostración de las leyes
de Kepler se basa en las leyes de Newton que enunciamos a continuación.
2 Leyes
de Newton
- Primera ley (ley
de la inercia): Todo objeto en estado de movimiento uniforme tiende a
permanecer en este estado de movimiento, a menos que una fuerza se le aplique.
- Segunda ley:
La relación entre la masa m de un objeto, su aceleración a
y la fuerza aplicada F es
- Tercera ley:
A toda acción corresponde una reacción de la misma magnitud y en
sentido contrario.
- Ley de la Gravitación
Universal: Todo objeto en el universo atrae a cualquier otro objeto con
una fuerza en dirección de la línea de los centros de los dos objetos,
que es proporcional al producto de sus masas e inversamente proporcional al
cuadrado de su distancia.
siendo G la constante de gravitación
universal. Si colocamos el origen de coordenadas en uno de los dos objetos,
tenemos
donde u es el vector
unitario en la dirección de la línea de los centros.
2.1 Demostración
de las leyes de Kepler a partir de las de Newton
Teorema 0
Los planetas se mueven
en planos.
Demostración:
Consideramos que el movimiento
del planeta se atiene a la 2a ley de Newton,
y que la única fuerza
que actúa sobre el planeta es la fuerza de atracción del Sol.
Coloquemos al Sol en el
origen de coordenadas.
Denotamos al vector posición
del planeta en el momento t como R=R( t) . Su velocidad v
se obtiene derivando el vector posición
y su aceleración a es
la derivada de la velocidad
Por la ley de la gravitación
universal,
|
F=- |
æ
ç
è
|
G |
mM
|| R|| 2
|
ö
÷
ø
|
u |
|
(2) |
donde u es el vector
unitario que va del Sol al planeta, es decir,
Igualando (1)
y (2) se obtiene
|
a=- |
æ
ç
è
|
G |
M
|| R|| 2
|
ö
÷
ø
|
u |
|
(3) |
por lo que el vector aceleración
es un múltiplo del vector posición u y se dirige siempre hacia
el Sol.
Consideremos el vector
conocido como el momento angular
del planeta.
Calculamos su derivada
|
|
d
dt
|
m( R×v) = m |
æ
ç
è
|
|
æ
ç
è
|
dR
dt
|
×v |
ö
÷
ø
|
+ |
æ
ç
è
|
R× |
dv
dt
|
ö
÷
ø
|
ö
÷
ø
|
=m( ( v×v) +( R×a) ) = 0 |
|
ya que a es un múltiplo
de u y por consiguiente un múltiplo de R.
Así que
esto significa que se conserva
el momento angular. Por lo que tanto R como [(dR)/dt]=v
son perpendiculares al vector
constante C y por tanto siempre están en un plano perpendicular a
C.
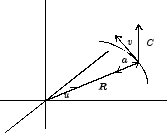
Figura 1
2.2 Demostración
de la segunda ley de Kepler
Como la curva que describe
el planeta es plana, podemos pensar que está en el plano XY y podemos parametrizarla
con coordenadas polares
donde el vector u es
un vector unitario
conocido como el vector unitario
en la dirección radial.
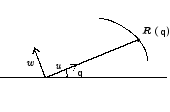
Figura 2
El ángulo q que forma el vector R
con el eje X depende del tiempo, es decir, q = q( t) .
El vector
se llama el vector unitario
en la dirección circunferencial.
Los vectores u y
w satisfacen las siguientes propiedades:
|
u^w, |
du
dt
|
=w |
dq
dt
|
, |
dw
dt
|
=-u |
dq
dt
|
|
|
Para probar la primera, calculamos
el producto escalar de u y w
|
u·w=( cosq,senq)·( -senq,cosq) = -cosqsenq+senqcosq = 0 |
|
Para la segunda, utilizamos
la regla de la cadena
|
|
du
dt
|
= |
du
dq
|
|
dq
dt
|
=(-senq,cosq) |
dq
dt
|
=w |
dq
dt
|
|
|
Elegimos el sistema de coordenadas
de manera que el valor inicial t=0 cuando r=|| R|| es mínimo, es decir,
cuando el planeta está en el perihelio, la posición más cercana
al sol y en este momento, el planeta se encuentra en el eje X, es decir,
q = 0.
Como r( q) alcanza su mínimo en
q = 0 entonces para t=0,
La velocidad del planeta
es la derivada de la posición:
|
v( t) = |
dR
dt
|
= |
d
dt
|
ru = r |
du
dt
|
+ |
dr
dt
|
u = r |
dq
dt
|
w+ |
dr
dt
|
u |
|
La aceleración del
planeta es la derivada de la velocidad:
|
a( t) = |
dv
dt
|
= |
d
dt
|
|
æ
ç
è
|
r |
dq
dt
|
w+ |
dr
dt
|
u |
ö
÷
ø
|
=r |
d
dt
|
|
æ
ç
è
|
|
dq
dt
|
w |
ö
÷
ø
|
+ |
dr
dt
|
|
dq
dt
|
w+ |
dr
dt
|
|
du
dt
|
+ |
d2r
dt2
|
u |
|
|
= r |
dq
dt
|
|
dw
dt
|
+r |
d2q
dt2
|
w+ |
dr
dt
|
|
dq
dt
|
w+ |
dr
dt
|
|
dur
dt
|
+ |
d2r
dt2
|
u |
|
|
= -r |
æ
ç
è
|
|
dq
dt
|
ö
÷
ø
|
2
|
u+r |
d2q
dt2
|
w+ |
dr
dt
|
|
dq
dt
|
w+ |
dr
dt
|
|
dq
dt
|
w+ |
d2r
dt2
|
u |
|
|
= |
æ
ç
è
|
-r |
æ
ç
è
|
|
dq
dt
|
ö
÷
ø
|
2
|
+ |
d2r
dt2
|
ö
÷
ø
|
u+ |
æ
ç
è
|
r |
d2q
dt2
|
+2 |
dr
dt
|
|
dq
dt
|
ö
÷
ø
|
w |
|
En (3)
vimos que a( t) es un múltiplo de u, así que su componente
circunferencial vale cero.
y por tanto,
|
a( t) = |
æ
ç
è
|
-r |
æ
ç
è
|
|
dq
dt
|
ö
÷
ø
|
2
|
+ |
d2r
dt2
|
ö
÷
ø
|
u |
| (7) |
Multiplicando por r ambos
lados de (6) obtenemos
|
r2 |
d2q
dt2
|
+2r |
dr
dt
|
|
dq
dt
|
=0. |
|
El lado izquierdo es
así que
Por otra parte, el área
barrida desde 0 hasta q generada por R=ru
es
|
A( q) = |
1
2
|
|
ó
õ
|
q
0
|
r2( f)df |
|
Por el teorema fundamental
del cálculo,
como q es función de t, de
(8) tenemos que
|
|
dA
dt
|
= |
dA
dq
|
|
dq
dt
|
= |
r2(q)
2
|
|
dq
dt
|
=k=constante, |
| (9) |
por lo que A( t) = kt+c para
alguna constante c. Como A( 0) = 0, entonces
|
A( t) = kt para una constante k |
|
así que si tenemos dos
intervalos de tiempo [ t1,t2] y [ t3,t4]
en los que t2-t1=t4-t3 entonces
|
A( t2-t1) = ( t2-t1) k=(t4-t3) k=A( t4-t3) |
|
lo que prueba la segunda ley
de Kepler.

Figura 3
Hasta este momento solamente
hemos utilizado que la fuerza F se dirige hacia el Sol, pero no hemos
utilizado la fórmula (2) en toda su extensión.
2.3 Demostración
de la primera ley de Kepler
Partimos de la ecuación
(7)
|
a( t) = |
æ
ç
è
|
-r |
æ
ç
è
|
|
dq
dt
|
ö
÷
ø
|
2
|
+ |
d2r
dt2
|
ö
÷
ø
|
u |
|
y de la ecuación (3)
|
a( t) = - |
æ
ç
è
|
G |
M
| R|2
|
ö
÷
ø
|
u |
|
Igualando los coeficientes
de u, llegamos a la ecuación diferencial
|
-G |
M
r2
|
=-r |
æ
ç
è
|
|
dq
dt
|
ö
÷
ø
|
2
|
+ |
d2r
dt2
|
|
| (10) |
De la ecuación (8)
tenemos
Para calcular el valor
de H procedemos como sigue:
Sustituimos en el momento
angular del planeta (4)
el valor de v de la
fórmula (2.2)
y obtenemos
|
h = m |
æ
ç
è
|
ru× |
æ
ç
è
|
r |
dq
dt
|
w+ |
dr
dt
|
u |
ö
÷
ø
|
ö
÷
ø
|
=mr2 |
dq
dt
|
( u×w)+mr |
dr
dt
|
( u×u) = mr2 |
dq
dt
|
uz+0 = mHuz |
|
donde uz
es el vector unitario ortogonal al plano donde se encuentran u y w.
Así que
Podemos suponer que H es
positivo orientando los ejes de manera que el planeta dé vueltas en sentido
positivo así que
Sea w=[1/r], entonces
|
|
dr
dt
|
= |
dr
dw
|
|
dw
dq
|
|
dq
dt
|
= |
æ
ç
è
|
- |
1
w2
|
ö
÷
ø
|
|
dw
dq
|
|
H
r2
|
=- |
dw
dq
|
H |
|
derivando nuevamente respecto
a t
|
|
d2r
dt2
|
=-H |
d
dt
|
|
æ
ç
è
|
|
dw
dq
|
ö
÷
ø
|
=-H |
dq
dt
|
|
d2w
dq2
|
=-H2w2 |
d2w
dq2
|
|
|
finalmente, el lado derecho
de la ecuación (10) se puede escribir como
|
-r |
æ
ç
è
|
|
dq
dt
|
ö
÷
ø
|
2
|
+ |
d2r
dt2
|
=-r |
æ
ç
è
|
H
r2
|
ö
÷
ø
|
2
|
-H2w2 |
d2w
dq2
|
=-w3H2-w2 |
d2w
dq2
|
H2 |
|
y el lado izquierdo
por lo que la ecuación
(10) se puede replantear como
esta ecuación tiene como
únicas soluciones
donde C y a son constantes. Eligiendo
el eje polar de manera que a = 0.
|
r = |
1
Ccosq+(GM)/(H2)
|
= |
H2
H2Ccosq+GM
|
= |
(H2)/(GM)
(H2Ccosq)/(GM)+1
|
= |
ep
ecosq+1
|
|
|
donde
La ecuación
es una cónica que tiene
un foco en el origen, en la que e es la excentricidad y p es la distancia
del foco a la directriz.
Las siguientes figuras
representan los tipos de cónicas que podemos encontrar.
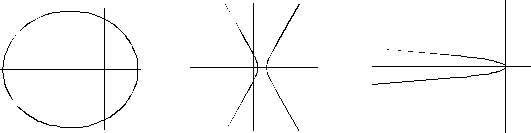
Figura 4
En el caso de los planetas,
sabemos que la órbita es cerrada, por lo que debe ser una elipse, así
que 0 < e < 1 lo que le impone restricciones a la constante C. Los cometas
u otros cuerpos atraídos por el sol pueden tener órbitas abiertas
en forma de parábola o hipérbola.
2.4 Prueba
de la tercera ley de Kepler
Podemos suponer que el
movimiento del planeta es en el sentido positivo, de modo que
y por tanto
Combinando (9),(11)
y (12) obtenemos
Integrando respecto al
tiempo T requerido para dar una vuelta completa a la órbita obtenemos
|
Area de la elipse= |
|| h||
2m
|
T. |
|
Si a y b son los semiejes mayor
y menor de la elipse, respectivamente, entonces
sabemos que
donde e es la excentricidad
de la elipse. Sustituyendo b en la ecuación anterior,
Calculemos ahora || h|| .
En la figura observamos
que r=a-c cuando q = 0 y r=a+c cuando
q = p.
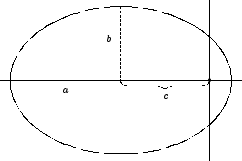
Figura 5
Haciendo
q = 0 en (15)
y sustituyendo el valor de r obtenemos
Análogamente si
q = p tenemos
sumando las dos ecuaciones
anteriores tenemos que:
Por otro lado, de (14)
y (13) se obtiene
de donde, despejando T de (16)
y elevando al cuadrado tenemos:
|
T2= |
4m2p2a4( 1-e2)
||h|| 2
|
. |
|
Despejamos || h|| 2
de (18) y la sustituimos en la ecuación anterior
y por la ecuación (17)
tenemos
por tanto,
quedando probada la tercera
ley de Kepler.
El factor de proporcionalidad
depende de las constantes G y M pero no depende de la excentricidad de la elipse.
En la tabla
aparece la excentricidad de
las órbitas planetarias, así como la distancia media del planeta al
sol medida en unidades astronómicas (U.A.). Una unidad astronómica es,
por definición, la distancia media de la tierra al sol. La distancia media
de un planeta al sol es el radio mayor de la elipse ( a) .
Si medimos el tiempo que
tarda un planeta en dar la vuelta alrededor del sol en años terrestres,
la constante de proporcionalidad de la tercera ley de Kepler es 1, es decir,
la fórmula de la tercera ley es
donde p es el período
y a es el radio mayor de la elipse.
Ejemplos
- Consideremos la órbita
de la Tierra. Si el Sol está en un foco, ¿a qué distancia
se encuentra el otro foco?
Solución:
Suponemos que la órbita
de la Tierra que es una elipse está centrada en el origen. El Sol es
uno de los focos.
Puesto que la excentricidad
de la órbita terrestre es
y a=1, entonces tenemos que
Las coordenadas de los focos
son
|
F( 0.017,0) y F¢(-0.017,0) . |
|
La distancia entre
los focos es 0.034 unidades astronómicas.
Observación:
Los focos se encuentran
muy cercanos
El diámetro menor
de la elipse es
|
b= |
Ö
|
a2-c2
|
= |
Ö
|
1-( 0.017) 2
|
» 0.99986 |
|
Puesto que el diámetro
mayor es a=1, entonces la elipse es casi un círculo.
- Consideremos la órbita
de Plutón. Si el Sol está en un foco, ¿a qué distancia
se encuentra el otro foco?
Solución:
Suponemos que la órbita
de Plutón que es una elipse está centrada en el origen. El Sol
es uno de los focos.
Puesto que la excentricidad
de la órbita de Plutón es
y a=39.44, entonces tenemos
que
|
c=( 0.25) ( 39.44) = 9.86 |
|
Las coordenadas de los focos
son
|
F( 9.86,0) y F¢(-9.86,0) . |
|
La distancia entre
los focos es 19.72 unidades astronómicas.
El diámetro menor
de la órbita de Plutón es
|
b= |
Ö
|
a2-c2
|
= |
Ö
|
( 39.44) 2-( 9.86)2
|
» 38. 188 |
|
Puesto que el diámetro
mayor es a=39.44, entonces la elipse es casi un círculo.
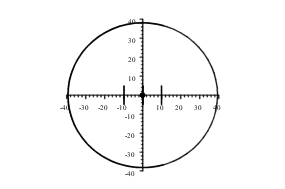
Figura 6
Bibliografía
- []
- Arizmendi H., Carrillo
A., Lara M., Cálculo, Addison-Wesley Iberoamericana, 1987
- []
- De Oteyza E., Lam E.,
Carrillo A., Hernández C., Ramírez A., Geometría Analítica
y Trigonometría, Pearson Educación, 2000
- []
- Marsden J., Tromba A.,
Cálculo Vectorial, Addison-Wesley Longman, 1998
- []
- O'Neill B., Elementos
de Geometría Diferencial, Limusa, 1972
File translated from
TEX by TTH,
version 2.80.
On 30 Mar 2001, 18:41. 








