1  El producto interior

Definición 1 Consideremos dos vectores a=( a₁,a₂,a₃) y b=( b₁,b₂,b₃) en R³. El producto interior de a y b denotado por a·b se define como

a·b=( a1,a2,a3) ·(b1,b2,b3) = a1b1+a2b2+a3b3.

Este producto se conoce como producto interior, producto punto o producto escalar.

Observación:

El producto interior de dos vectores es un escalar (número real).

Teorema 2 Si a=( a₁,a₂,a₃) , b=(b₁,b₂,b₃) y c=( c₁,c₂,c₃) son vectores en R³ y l es un número real entonces

i) a·a ³ 0.
ii) a·a=0 si y sólo si a=0, donde 0=( 0,0,0) es el vector nulo.
iii) la·b=l( a·b)
iv) a·b=b·a
v) a·( b+c) = a·b + a·c

Demostración:

i) Sabemos que




a·a=( a1,a2,a3) ·(a1,a2,a3) = a12+a22+a32,

como a_i² ³ 0 para i=1,2,3 entonces




a·a ³ 0.


ii) Si a·a=0 entonces




a12+a22+a32=0

y como a₁²+a₂²+a₃² ³ a_i² ³ 0 para i=1,2,3, se sigue que a_i²=0. Así a=0.

Si a=0 es claro que




a·a=0+0+0=0.


iii)




la·b = l( a1,a2,a3)·( b1,b2,b3)




= ( la1,la2,la3) ·(b1,b2,b3) = la1b1+la2b2+la3b3




= l( a1b1+a2b2+a3b3) = l( a·b)


iv)




a·b = ( a1,a2,a3) ·(b1,b2,b3) = a1b1+a2b2+a3b3 = b1a1+b2a2+b3a3 = b·a


v)




a·( b+c) = ( a1,a2,a3) ·( b1+c1,b2+c2,b3+c3) = a1( b1+c1) +a2( b2+c2)+a3( b3+c3)




= a1b1+a1c1+a2b2+a2c2+a3b3+a3c3 = a1b1+a2b2+a3b3+a1c1+a2c2+a3c3




= ( a1,a2,a3) ·( b1,b2,b3)+( a1,a2,a3) ·( c1,c2,c3) = a·b+a·c

Observación:

Como consecuencia de iii), iv) y v) tenemos:

Teorema 3

a·lb=l( a·b)

( b+c) ·a=b·a + c·a

Definición 0 Tomamos un vector a=( a₁,a₂,a₃) en R³. La norma del vector a, denotada por ||a|| se define como

|| a|| = ( a·a)[1/2],

es decir,

|| a|| = Ö   a12+a22+a32   ,

donde consideramos la raíz cuadrada no negativa.

Observación:

La norma del vector a representa la longitud del vector.

Teorema 4 Si a=( a₁,a₂,a₃) , b=(b₁,b₂,b₃) y c=( c₁,c₂,c₃) son vectores en R³ y l es un número real entonces

i) || a|| ³ 0.
ii) || a|| = 0 si y sólo si a=0.
iii) || la|| = | l||| a|| .
iv) a·b=|| a|| ||b|| cosq, donde q es el ángulo entre 0^° y 180^° formado por los vectores a y b.
v) | a·b| £ ||a|| || b|| . Desigualdad de Cauchy-Schwarz.
vi) || a+b|| £ || a||+|| b|| . Desigualdad del triángulo.

Demostración:

i) Se sigue del inciso (i) del teorema anterior y del hecho de que sólo tomamos la raíz no negativa.
ii) Si || a|| = 0 entonces




Ö   a·a   =0,

de donde a·a=0 y por el inciso (ii) del teorema anterior a=0.

Si a=0 entonces




|| a|| =   _____ Ö0+0+0   =0.


iii)




|| la|| = || ( la1,la2,la3) || = Ö   ( la1) 2+( la2)2+( la3) 2   = Ö   l2( a12+a22+a32)   = Ö   l2   Ö   a12+a22+a32   = | l| || a|| .

Observamos que la raíz no negativa de l² es |l| , o sea Ö{l²}=| l| .
iv) Sólo discutiremos el caso en que 0^° < q < 180^°. Consideramos el triángulo cuyos lados son a, b y el segmento de recta que une los extremos de los dos vectores y cuya longitud es || b-a|| .



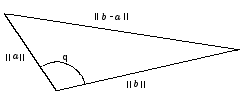
Figura 1

Aplicando la ley de los cosenos tenemos que




|| b-a|| 2=|| a||2+|| b|| 2-2|| a|| ||b|| cosq.

Como




|| b-a|| 2 =( b-a) ·( b-a) =b·( b-a) -a·( b-a) =b·b-b·a-a·b+a·a =b·b-2a·b+a·a =|| a|| 2+|| b||2-2a·b

Sustituyendo tenemos




|| a|| 2+|| b|| 2-2a·b=|| a|| 2+||b|| 2-2|| a|| || b|| cosq,

de donde




a·b=|| a|| || b|| cosq.


v)




| a·b| =| || a|| || b|| cosq| =|| a|| || b|| |cosq| £ || a|| || b||

ya que | cosq| £ 1. Por tanto




| a·b| £ || a|||| b|| .


vi) Consideremos || a+b|| ² entonces




|| a+b|| 2 =( a+b)·( a+b) =a·( a+b) +b·( a+b) =a·a+a·b+b·a+b·b =a·a+2a·b+b·b £ a·a+2| a·b|+b·b £ || a|| 2+2|| a|| ||b|| +|| b|| 2 =( || a|| +|| b|| )2

extrayendo raíz cuadrada de ambos lados de la desigualdad tenemos




|| a+b|| £ || a|| +||b|| .

Definición 5 Un vector u es unitario si || u|| = 1.

Observación:

Los vectores i=( 1,0,0) , j=(0,1,0) y k=( 0,0,1) son unitarios.

Teorema 6 Para cualquier vector a ¹ 0, el vector [(a)/(|| a|| )] es unitario.

Demostración:

|| a || a|| || = || 1 || a|| a|| = 1 || a|| || a|| = 1.

Teorema 7 Si a=( a₁,a₂,a₃) y b=(b₁,b₂,b₃) son vectores enR³ distintos del vector cero, entonces

a·b=0 si y sólo si a es perpendicular a b.

Demostración:

Si a·b=0 entonces como

a·b=|| a|| || b|| cosq

tenemos que

|| a|| || b|| cosq = 0

y como || a|| ¹ 0 y || b|| ¹ 0 entonces

cosq = 0.

Para valores entre 0^° y 180^° el coseno sólo se anula en

q = 90°,

es decir, los vectores son perpendiculares.

Inversamente, si los vectores son perpendiculares entonces el ángulo entre ellos es 90^°. Así

cosq = 0

y

|| a|| || b|| cosq = 0.

Como

|| a|| || b|| cosq = a·b

entonces

a·b=0.

Observación:

Resulta conveniente aceptar que el vector 0 es ortogonal a cualquier vector. Con esto el resultado anterior se generaliza y la condición a·b= 0 es entonces necesaria y suficiente para que dos vectores sean ortogonales entre sí.