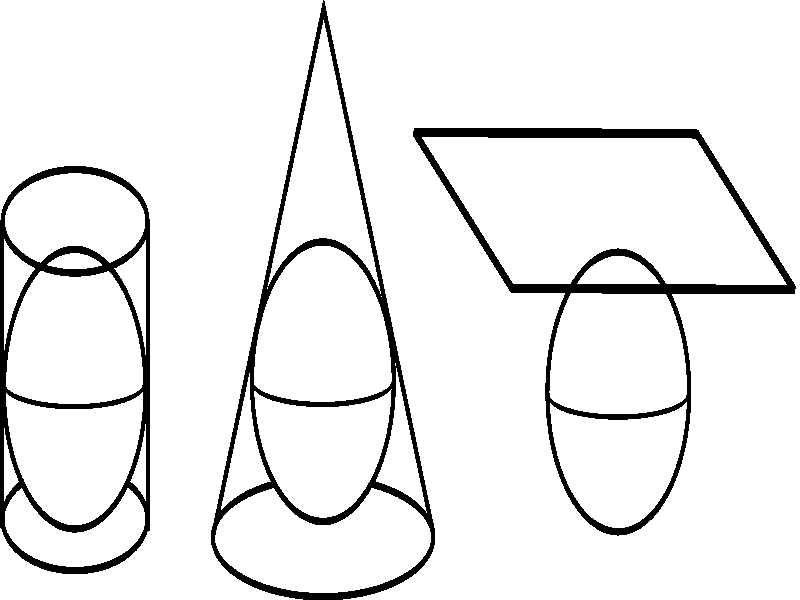
| Proyecciones. Introducción |
Proyectar quiere decir transferir
los puntos y las líneas de la superficie del globo al papel de acuerdo
a cierta técnica.
Históricamente, las proyecciones se derivaron proyectando primero de
la esfera a una forma intermedia la cual era de tal naturaleza que podía
ser desplegada sin distorsión. Esto ha quedado como un concepto útil
para categorizar y describir proyecciones de mapas. Las formas principales de
estas superficies intermedias son el cono, el cilindro y el plano mismo. La
ventaja de estas formas es debida a que su curvatura es en una dimensión
solamente y al desplegarse en un plano, no se distorsiona más. La superficie
a desplegar se pone en contacto con la esfera y se formula un conjunto de reglas
para la forma en que se transfieran los rasgos de la esfera sobre esa superficie.
Como ejemplos se tienen la superficie cilíndrica, la cónica y
la plana:
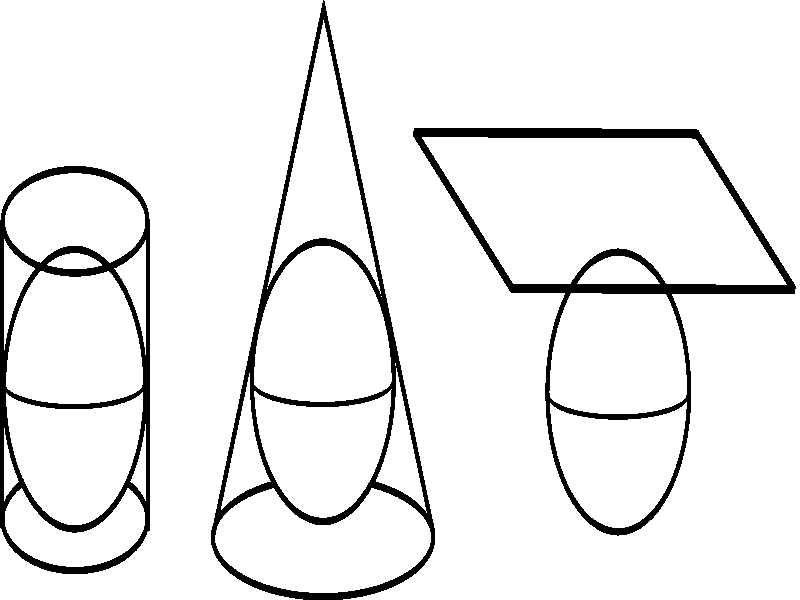
La proyección particular escogida para hacer un mapa dependerá del uso que se le quiera dar al mapa. Algunas proyecciones preservan las distancias relativas correctas, en todas las direcciones desde el centro del mapa (proyección equidistante), algunas muestran áreas iguales (proyecciones equivalentes o de igual área) o de formas similares (proyección conforme) a las del globo de la misma escala. Algunas son útiles para determinar la dirección. Estas son las propiedades que caracterizan una proyección. Muchas proyecciones de mapas se pueden construir usando una fuente de luz para proyectar las características del globo sobre una pieza de papel aún cuando, en la práctica, se hacen las operaciones matemáticamente más que con una luz. Otras proyecciones sólo pueden hacerse matemáticamente. No hay tal cosa como una proyección ideal o un mapa o una carta que sirva para todos los propósitos. Cada proyección debe sacrificar y tolerar la distorsión de una forma u otra.
Las proyecciones se clasifican en cónicas, cilíndricas o azimutales de acuerdo al método de proyección con una fuente de luz. Esto identifica el tipo de proyección. Muchas proyecciones que sólo pueden construirse matemáticamente se clasifican de acuerdo a este mismo esquema. Para el tipo de proyección elegida se escogerá la propiedad a conservar: distancias, áreas, formas,....
En una proyección cónica, por ejemplo, un cono de papel se coloca sobre el globo como un sombrero, tangente a él en alguna paralela y una fuente puntual de luz en el centro del globo proyecta los rasgos de la superficie sobre el cono. El cono se corta entonces a lo largo de un meridiano conveniente y se desdobla en una superificie plana en la forma de un círculo donde falta un sector. Todas las paralelas son arcos de círculos con un polo (el vértice del cono original) como su centro común y los meridianos aparecen como líneas rectas que convergen hacia el mismo punto.
En una proyección cilíndrica típica uno se imagina el papel enrollado como un cilindro alrededor del globo, tangente a éste a lo largo del ecuador. La luz viene de una fuente puntual en el centro del globo o, en algunos casos, de un filamento que corre de polo a polo a lo largo del eje del globo. En el primer caso es claro que los polos no pueden mostrarse en el plano ya que se proyectarían a lo largo del eje del cilindro hacia el infinito. En el otro caso, los polos se convierten en líneas que forman la base y el tope del mapa.
En una proyección azimutal una hoja de papel se coloca tangente al globo en un punto. La fuente puntual de luz puede localizarse en el centro del globo dando lugar a la proyección gnomónica. Cuando la fuente de luz está sobre la superficie del globo en un punto antípoda al punto tangente al plano, se tiene la proyección estereográfica. La fuente luminosa puede encontrarse en algún otro punto a lo largo de la línea definida por el punto tangente y el centro del globo; si el punto está infinitamente lejos del globo dará lugar a una proyección ortográfica.