Teselaciones con rombos.
Los rombos son un caso especial de
paralelogramos, en los cuales los cuatro lados son iguales, pero no necesariamente
forman ángulos rectos.
Los rombos se pueden acomodar en
el plano en filas, uno detrás de otro:

Si los ángulos
interiores de los rombos son de 30 y 60 grados, entonces también pueden
acomodarse agrupándolos formando hexágonos:
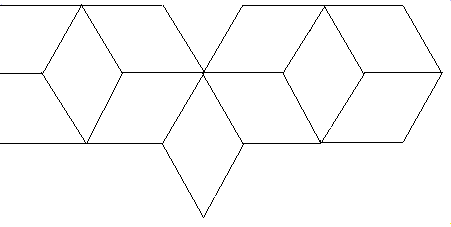
En esta sección veremos
los mosaicos del primer tipo y los otros los veremos en la sección de
mosaicos con hexágonos.
El rombo como paralelogramo.
Como el rombo es un paralelogramo,
entonces tiene las simetrías P1 y P2 del paralelogramo.
p1,
paralelogramo
Traslación horizontal y vertical,
1 unidad
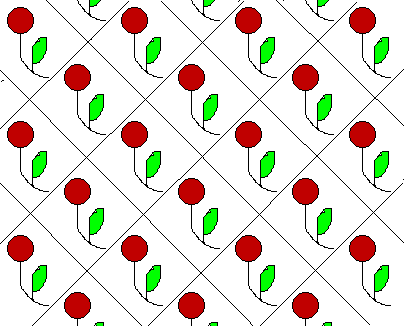
Oprime
aquí para
ver los mosaicos P1 formados por delfines.
p2,
paralelogramo
Rotación 180, 1/2 unidad

Oprime
aquí para
ver los mosaicos P2 formados por delfines.
cm,
rombo
Reflexión sobre una diagonal,
1/2 unidad
En este mosaico, las losetas
tienen una simetría de reflexión sobre una de las diagonales del
rombo. Se denomina cm (la m significa Mirror). Basta conocer la mitad
de un rombo para poder reconstruirlo todo mediante esta reflexión.
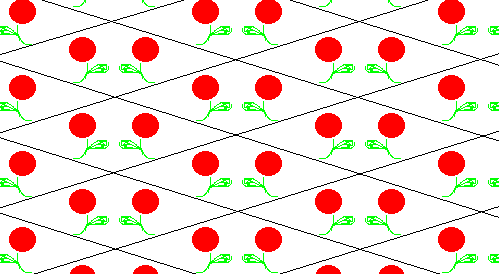
Oprime
aquí para ver los
mosaicos CM formados por delfines
cmm,
rombo
Reflexiones sobre ambas
diagonales del rombo, 1/4 unidad
En este mosaico las losetas
tienen dos simetrías de reflexión sobre ambas diagonales. Se denomina
cmm ( las 2 m's significan que hay dos reflexiones) . Basta conocer la cuarta
parte del rombo para poder reconstruirlo todo usando estas reflexiones. Observa
también que el mosaico es invariante bajo rotaciones de 180 grados con
centro en los centros de las losetas y en los vértices de ellas.







