
La Cicloide
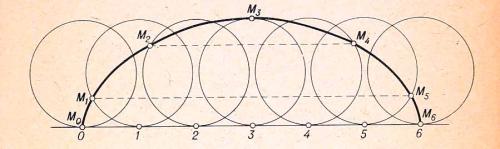
¿Cómo es una curva cicloide? Dibujémosla, es muy sencillo. En el borde inferior del pizarrón pongamos una regla y hagamos rodar sobre ella un aro o círculo (de madera o de cartón) apretándolo contra la regla y el pizarrón. Si fijamos en el aro o círculo un gis (en el punto de contacto con la regla), el gis describirá una curva denominada cicloide (que, traducido del griego, significa circular). Un giro del aro corresponde a un arco MM'M"N de la cicloide. Generemos el arco MM'M"N de una cicloide. Si el aro continua rodando, se obtendrán uno tras otro, los demás aros de la cicloide.

La primera referencia a esta curva está en un trabajo de Charles Bouvelles escrito en 1501 y a él es a quien se considera el verdadero inventor aun cuando la cicloide ya había sido estudiada por Nicolás de Cusa, en 1450. Cusa trató de encontrar el área de un círculo por integración. Galileo, a quien la curva debe su nombre, trabajó con la cicloide y habría mostrado, en 1599, que su área es casi tres veces la del círculo que la genera y sugirió que el arco de la cicloide debería ser apropiado para construir puentes{1}. Y así se hizo posteriormente. El padre Marin Mersenne (1588 -1648), en 1620, dio la primera definición de la cicloide y estableció sus propiedades obvias tales como que la longitud de la base es igual a la circunferencia del círculo que rueda. Intentó encontrar el área bajo la curva por integración pero falló y propuso el problema a otros matemáticos.
En 1639 Galileo escribió a Evangelista Torricelli (1608 -1647) sobre la cicloide diciéndole que había estudiado sus propiedades durante 40 años y que intentó encontrar el área bajo la curva comparando esa área con la del círculo que la genera por métodos mecánicos puesto que no pudo encontrar un método matemático para demostrarlo. Construyó arcos de cicloide y círculos de metal y los pesó, encontrando que la razón de los pesos era de aproximadamente 3 a 1 pero decidió que no era 3 exactamente, de hecho, aventuró el comentario de que la razón no sería un número racional, equivocadamente.
El estudio de la geometría de la cicloide y sus propiedades continuó pero su estudio sistemático comenzó con Blaise Pascal (1623 -1662). Según cuenta la historia, él sufría de dolores de muelas y otros achaques la noche que empezó a 'rumiar' sobre la cicloide pero, a tal punto se distrajo pensando en ella que sus penas desaparecieron. Entendió con esto que La Divinidad estaba de acuerdo y que autorizaba un último desliz matemático antes de dedicarse por completo a la vida mística. Resolvió, en ocho días, el problema de calcular el área de una sección generada por cualquier línea paralela a la base de un sólido; los volúmenes generados al rotar los sólidos alrededor de su eje o base; sus centros de gravedad y otros resultados varios. Para lograr lo anterior requirió integrar varias funciones trigonométricas, una operación que nunca antes se había intentado y que, por supuesto, no fue reconocida en su tiempo (1658) como parte del Cálculo.
También resolvió el problema del volumen y superficie del sólido de revolución formado al rotar la cicloide alrededor del eje XX'.
Pascal emitió un comunicado (no con su nombre sino con el de Dettonville) invitando a la comunidad matemática de Europa a resolver estos problemas ofreciendo premios pero sólo recibió dos respuestas formales y ninguna lo suficientemente buena para ganar ningún premio. Otros cinco matemáticos, entre ellos Sir Christopher Wren (1632 -1723), le respondieron sin entrar a la competencia. La mejor contribución fue la de Wren quien encontró la longitud del arco de la cicloide. Pascal publicó sus soluciones a los problemas planteados junto con una extensión del trabajo de Wren que Pascal mismo encontró.
El descubrimiento más famoso con respecto a la cicloide llegó en 1696, cuando Johann Bernoulli decidió determinar la ecuación de la trayectoria de descenso que seguiría una partícula que cae libremente de un punto a otro en el tiempo más corto, problema que, como dijimos en la sección de La Braquistócrona, resolvió Newton de manera definitiva.
{1} En una carta a Cavalieri (Feb 24 de 1640) Galileo dice de la cicloide: "Se me ocurrió describir esa línea arqueada hace más de 50 años, la admiraba como una curva muy graciosa que debería ser apropiada para los arcos de un puente". (Citado en Stilman Drake, 'Galileo at work', Publicaciones Dover, p. 406.)