
En el resto de este trabajo tendremos que analizar las órbitas de diferentes puntos en el dominio de nuestra función logística, así que es conveniente hacer claro un truco que estaremos utilizando asiduamente.
Supongamos que poseemos la gráfica
que describe nuestra función una vez que se ha dado el valor para
el parámetro r en la expresión 1.7. La gráfica se verá como
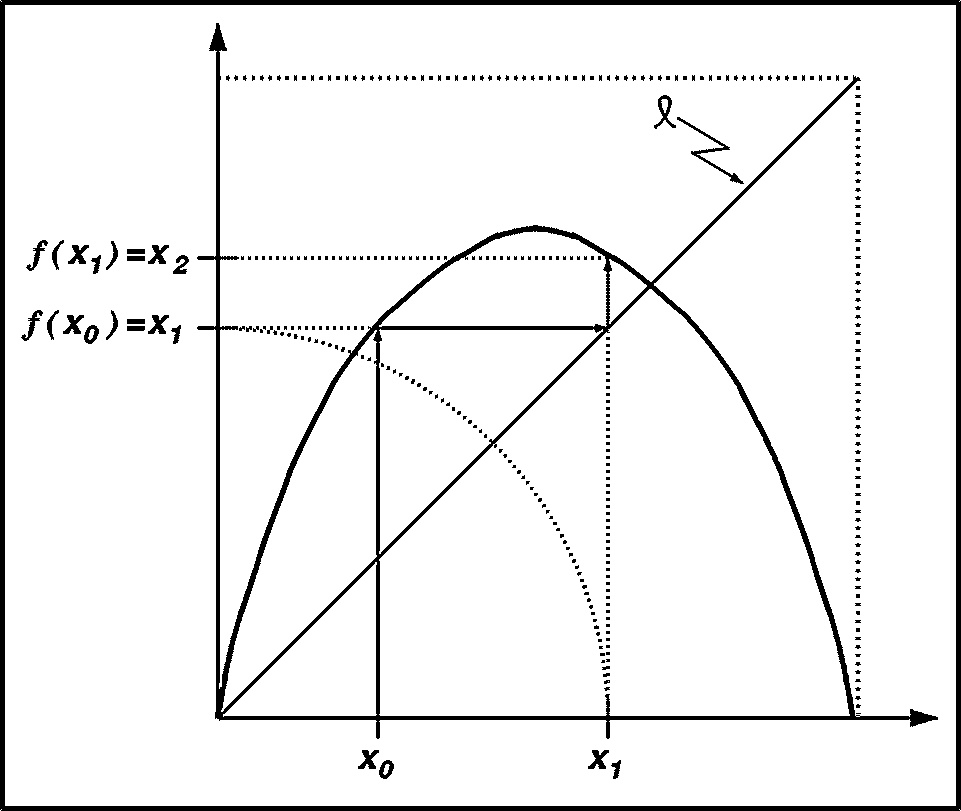
la que se muestra en la figura 1.1. Ahora supongamos
que queremos seguir la secuencia de puntos en la órbita de un valor
determinado del dominio de la función, digamos x0
Î [0,1]. Como dijimos la órbita
de x0 está dada por:
siempre xn es obtenida a partir de xn-1 aplicando la misma función, repitiéndola
o, para hablar propiamente, iterándola.
x1
=
4 r x0
( 1 - x0 )
x2
=
4 r x1
( 1 - x1 )
x3
=
4 r x2
( 1 - x2 )
:
Pues bien, si nos fijamos en el valor que se obtiene para x1 a partir de x0 en la gráfica, éste corresponde al punto en el eje vertical (ordenadas) que corresponde a la altura que tiene la función en x0. Si ahora queremos iterar el proceso evaluando la función en x1, formalmente tendríamos que fijarnos en el valor x1 en el eje horizontal (abscisas), gráficamente lo que haríamos es apoyar la punta de un compás en el origen donde cruzan los ejes y abrirlo hasta llegar a la altura x1 para luego trazar un arco y localizar a x1 en el eje de las abcisas. Luego podemos fijarnos en la altura que la función tiene en x1 y habremos localizado x2. Pero si observamos la figura 1.1 nos percataremos de que hay un atajo, en vez de localizar x1 sobre el eje de las ordenadas y luego "bajarlo'' con el compás, podemos trazar la horizontal que pasa por x1 en la gráfica de la función hasta topar con la recta l, que no es otra que la recta que pasa por el origen a 45o, y=x (la identidad), y luego "rebotar en ella'' hacia arriba hasta volver a encontrar a la gráfica de la función para localizar x2. Podemos repetir este proceso tantas veces como sea necesario, "rebotando'' en la diagonal y localizando todos los puntos en la órbita de x0. Al resultado gráfico de aplicar este proceso se le denomina diagrama de telaraña, por razones que pronto serán evidentes.