Hace mucho tiempo, más de 100 años, se encontró este papiro en la tierra de los faraones:

(Tomado de www.thebritishmuseum.ac.uk/egyptian/ea/gall/rhind.html)

Es el papiro Rhind. Debe su nombre al egiptólogo escocés Alexander Henry Rhind quien lo compró en Luxor en 1858; a su muerte fue adquirido por el Museo Británico, donde se conserva. Es un rollo como de 6m de largo y de 1/3m de ancho que se escribió cerca de 1,650 a. C. por el escriba Ahmes, un clérigo del rey Raaus quien copió un documento que era 200 años más antiguo. Esto da una fecha para el papiro original de 1,850 a. C. pero algunos expertos creen que el papiro Rhind se basa en un trabajo que se remonta a 3,400 a. C.
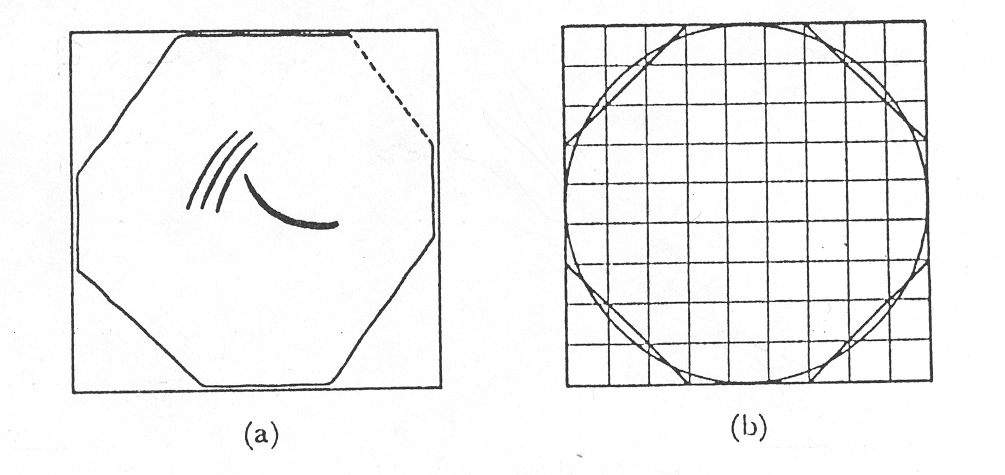
En el se encuentran 87 problemas matemáticos seguidos de su solución. Los problemas 41, 42, 43, 48 y 50 se relacionan con la cuadratura del círculo. En el problema 50 el escriba propone una regla para encontrar el área de un círculo de manera aproximada. El problema 48 contiene un dibujo muy famoso de un cuadrado con un octágono inscrito, (a), que nos ayuda a entender el problema 50.

El problema número 48 dice

No importa qué sean los khets, puedes pensar que son 9 metros, 9 kilómetros o simplemente 9 unidades.
¿Qué hicieron los egipcios para resolver este problema? Lo difícil era calcular el área del círculo. Veamos. El área de un círculo con diámetro 9 khets, calculándola como ahora sabemos, es aproximadamente 64 khets cuadrados; el área del cuadrado que lo contiene, de 9 khets de lado, es 81 khets cuadrados. Hay mucha diferencia entre una y otra. ¿Cómo aproximaron ellos el área del círculo?

En el problema 50 Ahmes presenta la regla para construir un cuadrado de área casi igual a la del círculo: