La dimensión fractal

En realidad existe más de una dimensión fractal, que en la mayoría de los casos dan el mismo resultado. Aquí definiremos sólo dos de ellas.

Primera definición (intuitiva)

La dimensión es el número de coordenadas para describir la ubicación de un punto en la figura:

Una línea tiene dimensión uno: basta dar la distancia de uno de sus extremos para fijar un punto en ella. Esto se usa en las carreteras: se toma como referencia una ciudad (es decir un punto extremo de la línea) y se ponen señales que nos indican la distancia a la que nos encontramos de esa ciudad.
Un rectángulo tiene dimensión dos: Para ubicar un punto en el recta, basta con dar las distancias de dos de sus lados. Esto se usa en ciudades donde las calles forman una rejilla para ubicar lugares específicos. Por ejemplo, "nos vemos en el cruce de la calle 56 Oeste con la 5ª Avenida".
Una esfera también es una figura geométrica de dos dimensiones. En la tierra se da longitud y latitud para ubicar una posición exacta: la ciudad de México tiene latitud 19.24 Norte y longitud 99.09 Oeste.
Un cubo, una esfera o un cilindro tienen tres dimensiones: hay que dar la altura y luego dos coordenadas para ubicar el punto a esta altura.

Esta definición intuitiva no es del todo satisfactoria. Vimos en la curva final que hay curvas que llenan un área completa y por lo tanto una "coordenada" es suficiente para indicar la posición de un punto en un cuadrado. Esto preocupó a los matemáticos y por ello hicieron varios esfuerzos para mejorar la definición. Describimos uno de estos esfuerzos en la dimensión topológica.

La dimensión fractal

Para medir el área de una figura como la mancha azul de abajo se puede usar el siguinte método: se cubre la figura con cuadrados de lado r y se cuenta el número de cuadrados necesarios.

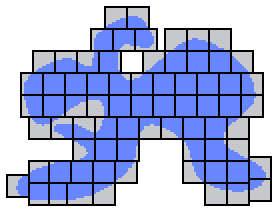
En nuestro ejemplo se necesitaron 72 cuadrados para cubrir la figura azul. Los cuadrados cubren un área de 72*r^2, mostrada en gris y azul. El área gris muestra la diferencia entre el área de la figura azul y 72*r^2.
Al usar cuadrados más chicos podemos reducir el área gris: la diferencia (el error) entre el área de la figura y el área medida con los cuadrados. Necesitaremos más cuadrados, digamos N y el área cubierta por los cuadrados será N * r^2.
En conclusión: el valor de N * r^2 se aproxima al área de la figura azul si reducimos el lado del cuadrado r hacia cero.

Usaremos este método para medir el área de un segmento. Has leido bien: área y no longitud. Deberíamos obtener que el segmento no tiene área, es decir que su área es cero.

Si el segmento azul tiene una longitud L necesitaremos al menos N = L / r cuadrados de lado r para cubrirlo completamente. Para ser precisos: N es el primer número entero que es igual o más grande que L / r (en general L / r no va a ser un número entero y no tiene sentido decir "Necesitamos 8.3 cuadrados", pero si L / r = 8.3 entonces necesitaremos 9 cuadrados).
Por ello obtenemos que N es menor que L / r + 1 y el área cubierta por los cuadrados es menor que ((L / r) + 1) * r^2 = L * r + r^2.
Pero L * r + r^2 se aproxima a cero si acercamos r a cero. Por lo tanto calculamos que el área del segmento es cero, lo que esperabamos.

Podemos modificar el cálculo: observemos que si multiplicamos el número N por r y luego acercamos N a cero entonces N * r se acerca a L, la logitud del segmento. En otras palabras: podemos calcular la longitud del segmento usando este mismo método, sólo que consideramos la expresión N * r en vez de N * r^2 cuando r se acerca a cero.

De la misma manera podrímos calcular la longitud de la mancha de arriba. Para ello tendríamos que observar qué pasa con el valor de N * r si acercamos r a cero. No es díficil ver que N * r rebasa cualquier número finito, en otras palabras: N * r "se aproxima a infinito", la longitud de la mancha es infinita.

Calculamos ahora longitud y área de un fractal:

Resulta que tiene una longitud infinita pero un área cero. Resumimos:

	Longitud	Area	Dimensión
Se mide con:	N r*	N r^2*
Mancha	infinita	finita, pero no cero	2
Segmento	finita pero no cero	cero	1
Fractal	infinita	cero	?

El truco consiste en considerar el comportamiento de N * r^D cuando acercamos r a cero para diferentes x. Podemos medir el "contenido" de un segmento (su longitud) si consideramos D = 1 y podemos medir el "contenido" de la mancha (su área) si consideramos D = 2.
En el ejemplo de la curva de Koch (el fractal de arriba) obtenemos que para D = 1.2618 la expresión N * r^D se aproxima a un valor positivo no cero. Por ello, el contenido de la curva de Koch se puede medir en la dimensión D = 1.2618.

La dimensión de similitud

La dimensión fractal es difícil de calcular. En los ejemplos que provee el simulador de fractales, los fractales son "autosímiles", es decir, una parte de él es una copia de la figura entera a una escala mayor. Esto puede ser utilizado para calcular la dimensión de similitud, que en muchos casos da el valor correcto para la dimensión fractal.

Tomamos de nuevo la curva de Koch. La podemos dividir en 4 partes iguales a toda la figura, a una escala 1/3.

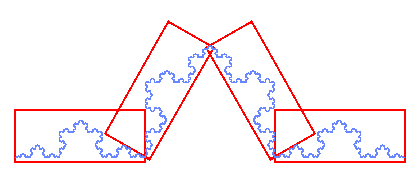
Si medimos la longitud L(a) de la curva con un compás de abertura a y lo comparamos con la longitud L(a/3) que obtenemos si medimos con una tercia de abertura, obtenemos

L(a) = 4/3 * L(a/3) Cada vez que medimos con una precisión tres veces mayor, obtenemos que la longitud se multiplica por 4/3. La ecuación tiene como solución: L(x) = a^x con x = log 4 /log 3 - 1 = 1.2618 - 1 = D - 1 (D la dimensión fractal de la curva de Koch).

En conclusión: para calcular la dimensión de similitud hay que calcular

log N / log e donde N es el número de partes similares y e el factor escala (cuántas veces hay que ampliar cada parte para obtener toda la figura). Si hay partes a diferente escala el cálculo es un poco más complicado.

La dimensión de similtud indica bien la dimensión fractal si en el fractal no hay intersecciones, es decir puntos por donde pase el fractal más de una vez.