Con este razonamiento obtenemos 63/81
D2 para el área del octágono y 64/81 D2
para el área del cuadrado cuyo lado vale D-1/9D, es decir, para el área
del círculo aproximado de acuerdo a la regla. Muy parecidas ¿no?
Con su regla los egipcios aproximaban el área de un círculo por
medio de un cuadrado.
Esto nos dice que los egipcios ya se preocupaban por calcular el número
p, indirectamente, es decir, por calcular el área de un círculo
cuando se conoce su diámetro. Acabamos de calcular el área de
un círculo casi igual al área de un cuadrado.Tenían un
método que, sin ellos saberlo, les daba un valor de p
más o menos razonable, según los conocimientos actuales.
Pero los griegos, que desarrollan las matemáticas de manera sistemática,
querían resultados precisos. ¿Qué tan aproximado fue ese
valor? ¿Cómo se podría mejorar?
Calculemos el valor de los egipcios para p.
Con la fórmula que en primaria nos enseñaron sabemos que el área
del círculo es
Área círculo = pr2
Por otro lado, el área de un círculo casi igual al área
del cuadrado (la calculada con la regla egipcia) tendría que ser igual
a la calculada como nos enseñaron en primaria, se tiene entonces:
| Área del cuadrado = | Área del círculo |
| (D- 1/9D)2 = | pr2 |
| (8/9D)2 = | p(D/2)2 |
| 64/81 D2 = | p/4 D2 de donde |
| 64/81 = | p/4 |
| 4*(64/81) = | p |
esto nos da el valor aproximado para p:
p=
(4*64)/81= (4/3)4 @
3.1605
Los egipcios encontraron este valor aproximado para
p. No es lo que sabemos que vale pero es cercano, no está tan mal, ¿no crees? El
número p
es la relación de la circunferencia al diámetro del círculo,
es decir, el diámetro cabe p veces en la circunferencia
del círculo.
Con nuestro valor moderno para p
un círculo de diámetro 9 khets tendría un área de
63.6174 setat (khets cuadrados) de manera que el valor de los egipcios, 64,
tuvo un error menor del ¡0.6%!
¿Cómo podemos calcularlo?¿de
dónde sale esa formulita de pr2?
y ¿qué justificación hay de que exista un número
que multiplicado por el radio al cuadrado me de el área del círculo?.
Tomemos un círculo. Si quiero calcular su área ¿cómo
le hago?. Una forma es: ¿qué tal si voy acercándome poco
a poco a lo que me interesa? ¿qué tal si tomo un pentágono
regular (esto es, con sus cinco lados iguales)

y veo cómo se compara su área con la del círculo?.
Calcular el área del pentágono es muy fácil. Como todos
sus lados son iguales, si desde el centro trazo líneas a los vértices,
obtengo cinco triángulos iguales. Llamemos h
a la altura del triángulo y b a su
base:
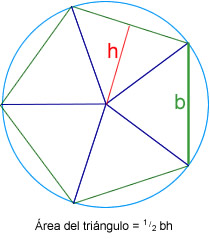
y sabemos que
Área triángulo = ½ b*h
de donde
Área pentágono = 5 *Área del triángulo
=
5 *(½) b*h
=
(½ h) 5* b
= (½ h) * perímetro del pentágono
Entonces, ¿qué pasa si en vez de un pentágono es un hexágono
o un heptágono o cualquier polígono regular?