La primera pregunta que se hace uno es ¿de dónde sacaron los egipcios esa regla para aproximar el área de un círculo?, ¿por qué esa fórmula?
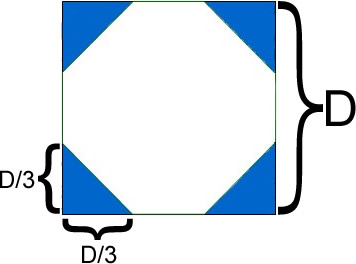
Realmente no se sabe de dónde la obtienen, aunque se especula que fue por medios empíricos. El diagrama del problema 48 representa un cuadrado con los lados trisecados que sirve de explicación. Es casi seguro que notaron que si se eliminan las áreas sombreadas del cuadrado original (las áreas que quedaban fuera del octágono) el lado del cuadrado debía tener un valor 8 en el caso que el diámetro fuera 9. Esto se ve, claramente, en la animación que sigue. Al generalizar sus resultados llegaron a la regla. El área del círculo es aproximada por el área del cuadrado de 8 khets ya que es el área aproximada del octágono inscrito. Por supuesto que el escriba supo que su método no era exacto pero le permitía encontrar un círculo de área casi igual a la del cuadrado. Es aproximada también porque, como muestra la ingeniosa animación, en la esquina superior izquierda se empalman dos unidades de área.
Es claro que el cuadrado que resulta al eliminar las regiones sombreadas tiene 8 unidades por lado. El área de este cuadrado se aproxima a la del círculo de diámetro 9 unidades. ¡Buen trabajo! Pero, además de interés gratuito por calcular, ¿habrán tenido los egipcios alguna otra razón para calcular el área de un círculo? Sí, querían resolver problemas prácticos. Querían calcular el volumen de los silos cilíndricos en donde almacenarían los granos de sus cosechas. Al conocer el área del círculo sólo tendrían que multiplicar por la altura del cilindro para encontrar el volumen. Los depósitos rectangulares no les representaban problema de cálculo pero sí de eficiencia y pensaron que en un depósito cilíndrico de la misma altura que uno cuadrangular, podrían almacenar más granos. ¿Qué tan acertados estaban los egipcios en su conjetura...? ¿Cómo podrías tú saber cuál de los depósitos, el cilíndrico o el rectangular, contiene más granos? En tanto, continuemos calculando areas.
El área del octágono se calcula muy
fácilmente porque es el área del cuadrado menos el área
de los cuatro triángulos. Los egipcios no la calcularon directamente
pero nosotros vamos a hacerlo, por curiosidad, y la compararemos con el área
del círculo calculada con la regla.

Sabemos que los triángulos tienen base y altura un tercio del diámetro
y sabemos que el área de los triángulos es un medio de la base
por la altura.
Área de un triángulo = ½ (D/3 * D/3) = ½ (D/3)2
Calcula el área del triangulo (no olvides
que tienes cuatro) y réstasela al área del cuadrado (diámetro
al cuadrado, ¿recuerdas?)
| Área octágono | =Área cuadrado | - 4 Área triángulo |
| = D2 | - 4*(D/3 *D/3)/2 | |
| = D2 | - 2(D2/9) | |
| = 7/9 D2 | ||
| = 63/81 D2 |