El área de este polígono siempre va a ser más chica que el área del círculo, pero se parecerá cada vez más a ella.

Ahora calculemos el área dentro de ese polígono.
Si el polígono se llama P, de acuerdo a lo que hicimos antes, el área va a ser ½ de la altura del triángulo que se forme (sin importar cuántos triángulos haya), multiplicada por el perímetro.

Área dentro del polígono  =	½ h * perímetro del polígono, esto es,
Área P =	½ h * perímetro P

Esta es la manera en que pensaban los griegos y más aún, se preguntaban ¿qué pasa si divido las bases de los triangulos?, ¿si divido los lados del polígono cada vez más y más?, ¿qué pasa si me voy al extremo de un número grandísimo de lados? y, ¿si hago esto un número infinito de veces?...
Lo que sucederá es que tendremos lados "casi pegados" al círculo, y la h se parecerá más al radio.

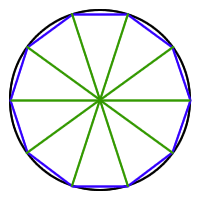
Entonces, en el límite de un número infinito de lados, la altura del triángulo tiende a ser el valor del radio, es decir, tiende al valor de r. Esto se escribe como: lim h ® r.

Si ese razonamiento es correcto, entonces la longitud de la circunferencia es igual al límite de los perímetros conforme los polígonos tienen más y más lados, es decir, conforme se parecen más a la circunferencia, en ese caso ideal, en el límite, el área del polígono es el área del círculo. Dicho de otra forma,
lim Área del Polígono = área círculo

Entonces
Área círculo   = lim [área polígono inscrito]
                        = lim [½ h * perímetro P]      y como h tiende a r y el perímetro tiende a la circunferencia,
                                                                               al valor C, en el límite, escribimos,

Área círculo   » [½ r * C].

Sabemos, por su definición, que C = pD, entonces, con la aproximación, tenemos
Área círculo = ½ r * pD
                      = ½ r * p2r
                      = pr²