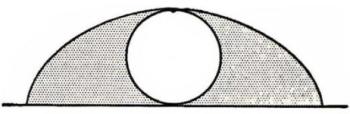
Propiedades de la Cicloide
La cicloide es una curva hermosa con propiedades sorprendentes. Sabemos, por ejemplo, que dada la naturaleza del número p, el área de un círculo puede expresarse solamente de manera aproximada, sin embargo, con la ayuda de la cicloide se puede construir un área exactamente igual al área de un círculo dado. Basándose en el hecho de que la longitud de una cicloide, de cúspide a cúspide, es igual a cuatro veces la longitud del diámetro del círculo que la genera, se puede mostrar que el área encerrada por la porción de la cicloide entre las dos cúspides y la línea recta que los une, es igual a tres veces el área del círculo. De esto se sigue que el espacio encerrado (la región sombreada en la figura) en cualquier lado del círculo que está en el centro es exactamente igual al área del círculo mismo.

En 1630, Mersenne, habría sugerido a la comunidad matemática encontrar la cuadratura de la cicloide y fue así que Gilles Personne de Roberval (1602 -1675) se dio a la tarea de calcularla comprobando que el área contenida en un arco de cicloide es tres veces el área del círculo que la genera. Mersene había propuesto el problema del área a Roberval en 1628 pero falló hasta lograrlo en 1634, tan orgulloso estaba de sus resultados que escribió a Descartes diciéndoselo, a lo cual Descartes contestó: Muy bonito, no lo había notado, pero, no debería causar ningún problema a cualquier geómetra moderadamente hábil. Descartes retó a Roberval a encontrar un método para dibujar una tangente a la cicloide cuando ya él mismo lo había encontrado. Roberval falló pero Pierre de Fermat, quien estaba incluido en el reto, triunfó.
Por su parte, Torricelli, de manera independiente, calculó el área de la cicloide, y Vincenzo Viviani (1622 - 1703), encontró un método para construir una tangente a la misma. Es importante señalar aquí que, tanto el problema de las cuadraturas como el de construir tangentes a las curvas eran los problemas matemáticos del momento; hacía falta una teoría geométrico-algebraica de curvas para resolverlos de manera general. No sería sino hasta la invención del cálculo por Newton y Leibniz que se reconocerían como problemas inversos: uno es un problema diferencial y el otro, integral.
Ahora, observa una cicloide, invierte uno de los arcos, toma un tramo y ...¡tienes a la braquistócrona!
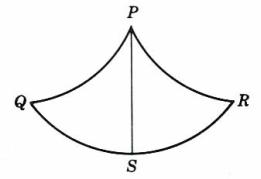
No obstante las propiedades mencionadas, hay otras para esta curva. Seguramente habrás oído hablar de Christiaan Huygens (1629 -1695), un matemático holandés que construyó relojes de péndulo. El era, en realidad, un científico de renombre y reputación internacional a quien se recuerda, sobre todo, por el principio que lleva su nombre en la teoría ondulatoria de la luz. Fue maestro de Leibniz y anticipó muchas de las ideas del cálculo infinitesimal pero le disgustaba el "Kalkül". El sabía también que las oscilaciones de un péndulo simple no son estrictamente isócronas (es decir, que tarden lo mismo) sino que dependen del tamaño del columpio. En otras palabras, si un objeto se coloca sobre el lado de un recipiente redondo invertido y se suelta, el tiempo que le toma llegar al punto más bajo será casi (pero no exactamente) independiente de la altura desde la cual se suelte, lo cual restaba exactitud a los relojes. Sucedió que Huygens inventó el reloj de péndulo casi al mismo tiempo que Pascal convocara al concurso de la cicloide, en 1658. Se le ocurrió considerar qué pasaría si se sustituyera el recipiente esférico por uno cuyo sección transversal, en lugar de ser redonda, fuera un arco de cicloide invertida. Se maravilló al encontrar que, para tal recipiente, el objeto llegará al punto más bajo en exactamente el mismo tiempo; sin importar desde qué altura de la superficie interior del recipiente se suelte. Es decir, la partícula exhibe movimiento armónico simple y el periodo es independiente de la altura inicial. En otras palabras, en su péndulo, el periodo de oscilación es independiente de su amplitud. La curva cicloide es, en realidad, una tautócrona: esto es, sobre un arco cicloidal invertido, un objeto deslizará desde cualquier punto a la base, en exactamente el mismo tiempo, sin importar en qué punto comience. Un gran logro de Huygens fue demostrar que la cicloide es la única curva que tiene esta propiedad. De esta propiedad de la cicloide se valió Huygens, en 1673, (en Horologium oscillatorium) para diseñar los péndulos isócronos con un aditamento que fuerza al péndulo a columpiarse en un arco de cicloide. Pero ¿cómo se le hace para que un péndulo oscile en un arco cicloidal? Esto fue un descubrimiento precioso de Huygens. Si desde un punto P en la figura se suspende un péndulo cuya longitud es igual a la longitud de uno de los dos semiarcos cicloidales PQ y PR, la punta del péndulo se columpiará en un arco que es un arco de la cicloide QSR de exactamente el mismo tamaño y forma que la cicloide de la cual los arcos PQ y PR son parte. En otras palabras, si el péndulo del reloj oscila entre quijadas cicloidales, será realmente isócrono. Sin embargo, pese a esta valiosa propiedad, un reloj así presenta tantos problemas de construcción que se hace impráctico. No obstante, el estudio de estos relojes le valió a Huygens descubrir una verdad matemática de capital importancia: la involuta de una cicloide es una cicloide similar, o, inversamente, la evoluta de una cicloide es una cicloide similar. Gracias a estas propiedades Huygens desarrolló una teoría general de evolutas. Su razonamiento va más allá del cálculo diferencial e integral y alcanza dominios nuevos del pensamiento.
Entre otras características, la cicloide es la catacáustica (¡vaya nombrecito!) de un círculo cuando los rayos de luz vienen de un punto sobre la circunferencia. Esto lo mostraron los Bernoulli en 1692. La cáustica de la cicloide, cuando los rayos son paralelos al eje YY', es una cicloide con el doble de arcos.
Pero los matemáticos no nada más trabajan para resolver problemas prácticos, más bien, todo lo contrario. Ellos crean, inventan, sin pensar para qué puede servir esto o lo otro. Así crearon una figura como la pseudoesfera (o seudoesfera). Les sirvió para explicar qué pasaría si, en nuestro mundo, las líneas rectas paralelas se doblaran es decir, que al prolongarse, se acercaran, o se alejaran, a diferencia de como nos enseñó Euclides. Esto es, crearon una geometría diferente a la de Euclides y necesitaron de la pseudoesfera para entenderla. Pero, ¿cómo es la pseudoesfera?. ¡Vamos a crearla a partir de curvas! Iniciemos con La Tractrix.
Nota: Las propiedades de la cicloide están ilustradas en la página