Otra manera de acercarse al problema de la cuadratura y a la solución de los otros dos problemas clásicos: el de la trisección del ángulo y el de la duplicación del cubo, es usando lo que los griegos llamaron cónicas. ¿Qué son las cónicas? Son las curvas que resultan de intersecar un cono con un plano.

Tomen un cono y lo cortan con un plano y dependiendo de cómo pongan el plano se obtiene una cónica diferente. Por ejemplo si tienen el cono y cortan de manera perpendicular al eje del cono, lo que se tiene es una circunferencia. Si inclinan un poco el plano entonces esa circunferencia se comienza a deformar y lo que se ve es una elipse, si lo inclinan más y más se llega a cierta posición en la que ya no vuelve a cerrarse la elipse y lo que obtenemos es una parábola. Son las curvas más simples después de la circunferencia. Los griegos sólo manejaban el concepto geométrico, no hay ecuaciones, las curvas cónicas se construyen simplemente intersecando conos.

Menecmo (~350 a. C.) fue un matemático destacado de la escuela de Cízico y a quien se atribuye el descubrimiento de las cónicas. Desde Apolonio de Perga (262-190 a. C.) "el gran geómetra", llevan el nombre de elipse, parábola e hipérbola.

El problema de la cuadratura de parábolas, por ejemplo, es parecido al del círculo. Pero ojo: la parábola es abierta, entonces no puedo preguntar por toda su área, sin embargo,... si sobre la parábola dibujo dos puntos opuestos, a la misma distancia del eje de la parábola y trazo la recta que pasa por ellos, perpendicular al eje, es decir, trazo un diámetro, ahora sí tengo un área definida entre la recta y la parábola y puedo preguntarme ¿cuál es el área de esa región?

Arquímedes (287-212 a.C.), uno de los matemáticos más grandes de todos los tiempos,

demostró que el área de una porción de parábola sí se puede calcular y de manera exacta. Primero resuelve el problema con medios mecánicos y, posteriormente, lo prueba de manera geométrica.

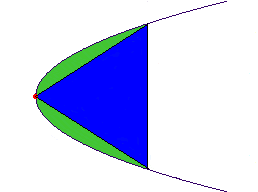
Si toman el punto rojo (el vértice de la parábola) y construyen el triángulo mostrado en azul, entonces, el área verde que está dentro de la parábola es 4/3 » 1.33... del área del triángulo.

Calcular el área del triángulo es fácil, y obtener 4/3 de ella es también sencillo, así que, resolvimos el problema. En este sentido, la parábola "se puede cuadrar". También se puede "cuadrar" con un rectángulo:

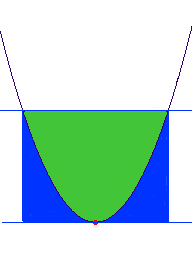
Cuando aprendas cálculo entenderás porqué el área de la parábola es 2/3 el área del rectángulo.

Pero para cuadrar el círculo Arquímedes usa su famosa Curva Espiral. Por otro lado, su contribución al cálculo de p utilizando polígonos es notable. Usando polígonos inscritos y circunscritos en un círculo, hasta de 96 lados, aproximó el área del círculo y, por tanto, aproximó el valor de p. Este fue el primer tratamiento realmente científico del cálculo de p. El cómo logró llegar tan lejos cuando no se contaba ni con números, es una muestra de su grandeza.

Sus aproximaciones son éstas
       3 10/71< p < 3 1/7 o bien
     3.14085 < p < 3.14286

que, por supuesto, fueron mucho mejores de lo que conocieron los egipcios. Su aproximación al valor de p es sorprendente. Durante cientos de años no hubo avances significativos en la búsqueda de p. Métodos similares al de Arquímedes se usaron en los 1,200 años siguientes, hasta el siglo 16.

El trabajo de Arquímedes hizo que los griegos sospecharan que el problema de la cuadratura del círculo se podría resolver, pero había otras razones...