Entre los esfuerzos por resolver el problema está el de

Hipócrates (s. V a. C.) quien demostró que la suma de las áreas de las medias lunas (llamadas lúnulas) que se forman en un semicírculo, es igual al área del triángulo inscrito.

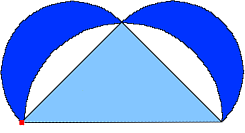Área Lúnulas = Área Triángulo

¿Cómo se construyen las lúnulas?

Como las lúnulas son porciones de un círculo y su área se puede calcular por medio del triángulo, resulta que, sí puedo cuadrar estas figuras semicirculares.)

Parecería que este es un camino para resolver el problema de la cuadratura del círculo. Pero Hipócrates supo muy bien que su trabajo no resolvía el problema; no obstante, la gente seguiría trabajando en él.