PUEMAC. Kepler. Introducción

Las leyes de Kepler son un ejemplo muy bueno de cómo se combinan diversas ramas de las matemáticas para poder llegar a una conclusión. En este caso se da la combinación de la geometría, el álgeba lineal, el cálculo diferencial e integral en una y varias variables, etc.

Como veremos más adelante, Kepler formuló sus leyes a partir de observaciones hechas por Tycho Brahe de la órbita de Marte, sin embargo, los recursos científicos de su época no le permitieron probar sus afirmaciones. Fue Newton quien lo hizo después de haber inventado el Cálculo Diferencial e Integral y de formular las Leyes de la Gravitación Universal.

En la sección Historia damos una breve historia de la concepción del Sistema Solar desde Aristóteles hasta Newton.

En las siguientes de prerequisitos damos las herramientas matemáticas utilizadas en las pruebas de dichas leyes como son: Producto escalar, Producto vectorial , Coordenadas polares, Ecuaciones diferenciales; de esta manera, el lector puede empezar a estudiar las demostraciones y si le hace falta entender mejor o profundizar en alguno de los conceptos utilizados, puede entonces recurrir a la sección correspondiente.

Leyes de Kepler

Aunque en los textos se muestran las órbitas de los planetas bastante alargadas, como la siguiente figura,

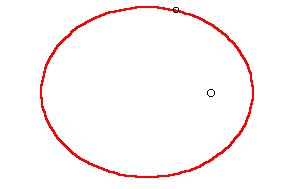
en realidad, las órbitas de la mayor parte de los planetas del Sistema Solar son prácticamente circulares. En la siguiente figura se muestra la forma de la órbita de la Tierra.

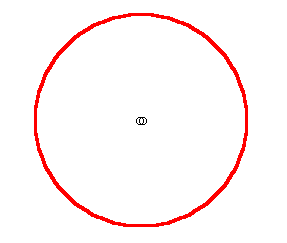
En la siguiente figura, las dos áreas sombreadas son iguales, así que el planeta tarda lo mismo en ir de A a B que en ir de C a D.

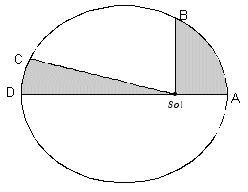
Esta ley relaciona el tiempo que tarda un planeta en dar la vuelta al Sol (su período) con su distancia media al Sol. Así que conociendo una de estas dos cantidades, es posible conocer la otra.

En la siguiente tabla se muestran las distancias de los planetas al Sol (medidas en Unidades Astronómicas) y su período (medido en años terrestres).

Una Unidad Astronómica es la distancia media de la Tierra al Sol y vale aproximadamente 150,000,000 Km

Planeta	Distancia al Sol	Período
Mercurio	0.837	0.24
Venus	0.723	0.61
Tierra	1	1
Marte	1.52	1.87
Júpiter	5.2	11.86
Saturno	9.54	29.47
Urano	19.18	84
Neptuno	30.06	164.81
Plutón	39.44	247.69

Puede comprobarse directamente la tercera ley de Kepler con los datos de cualquier planeta, por ejemplo, para Urano,

Las leyes de Kepler son un ejemplo interesante que muestra la manera en que diferentes ramas de las matemáticas, como son el álgebra lineal, la geometría analítica, el cálculo vectorial, las ecuaciones diferenciales, entre otras, se combinan para dar una demostración.

Cabe recordar que Kepler enunció sus leyes de manera empírica, y no fue sino hasta que Isaac Newton inventó el Cálculo Diferencial e Integral, casi un siglo después, que él mismo pudo demostrar las leyes de Kepler. Ver la demostración de las leyes de Kepler.

Angel Carrillo	Elena de Oteyza
Carlos Hernández	Emma Lam